统计学的基本概念和方法(统计学基础概念和方法)

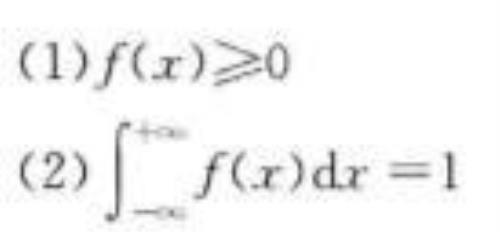
导语：统计学基础笔记：概念梳理5

对统计学基本概念的梳理，其中普通字体为贾俊平著《统计学(第六版)》中的重要概念，引用字体的内容为书中没有但相关的概念。

第5章 概率与概率分布

随机事件 / 偶然事件 random event

在同一组条件下，每次试验可能出现也可能不出现的事件。

必然事件 certain event

在同一组条件下，每次试验一定出现的事件。

不可能事件 impossible event

在同一组条件下，每次试验一定不出现的事件。

基本事件 elementary event

如果一个事件不能分解成两个或更多个事件，则这个事件称为基本事件或简单事件。

概率 probability

事件A的概率是描述事件A在试验中出现的可能性大小的一种度量，记事件A出现可能性大小的数值为P(A)，P(A)称为事件A的概率。

条件概率 conditional probability

当某一事件B已经发生时，事件A发生的概率，称这种概率为事件B发生条件下事件A发生的条件概率，记为P(A|B)。

独立性 independence

两个事件中无论哪一个事件发生并不影响另一个事件发生的概率，则称这两个事件相互独立。

概率函数 probability function

在同一组条件下，如果每次试验可能出现这样活那样的结果，并且把所有的结果都能列举出来，即把X的所有可能值x1,x2,...,xn都能列举出来，并且X的可能值x1,x2,...,xn具有确定概率P(x1),P(x2),...,P(xn)，其中P(xi)=P(X=xi)，称为概率函数，则X称为P(X)的随机变量，P(X)称为随机变量X的概率函数。

随机变量 random variable

离散型 discrete

如果随机变量X的所有取值都可以逐个列举出来，则称X为离散型随机变量。

连续型 continuous

如果随机变量X的所有取值无法逐个列举出来，而是取数轴上某一区间内的任一点，则称X为连续型随机变量。

概率分布 probability distribution

设有一离散型随机变量X，可能取值x1,x2,...,xn，其相应的概率为p1,p2

,...,pn，即P(x=xi)=pi(i=1,2,...,n)。将X=xi和P(X=xi)=pi列为两行，一一对应，则称列成的表格形式为离散型随机变量X的概率分布，其中，P(X=xi)=pi是X的概率函数。

期望值 expected value

离散型随机变量X的期望值定义为，在离散型随机变量X的一切可能值的完备组中，各可能值xi与其对应概率pi的乘积之和称为该随机变量X的期望值，记作E(X)或μ。

二项分布 binomial distribution

实际问题中，有许多试验与掷硬币的试验有共同的性质，它们只包含两个结果。这种随机变量所服从的概率分布通常称为二项分布。

贝努利试验 Bernoulli traials

具有如下特征的n次重复独立试验为n重贝努利试验【批：也称伯努利试验】，简称贝努利试验或贝努利试验模型：

包含了n个相同的试验每次试验只有两个可能的结果出现任一可能的概率对每一次试验是相同的试验是相互独立的试验的结果可以计数，即实验结果对应于一个离散型随机变量

概率密度函数 probability density function

当用函数f(x)来表示连续型随机变量时，我们将f(x)称为概率密度函数。概率密度函数应满足下述两个条件：

f(x)并不是一个概率，即f(x)≠P(X=x)，f(x)称为概率密度函数。

正态分布 normal distribution

在连续型随机变量中，最重要的一种随机变量是具有钟形概率分布的随机变量；人们称它为正态随机变量，相应的概率分布称为正态分布。

本文内容由小纳整理编辑！