抛物线开口大小到底要怎么具体量化这个问题(抛物线开口大小怎么看)

导语：抛物线开口大小，到底要怎么具体量化？这个内容课堂上一般不讲

我们都知道，抛物线y=ax^2+bx+c的开口是由a决定的。a的符号性质决定了开口的方向，当a>0时，抛物线开口向上，当a小于0时，开口向下。那你知道a是怎么决定抛物线的开口大小的吗？

通过具体的实例探究，不难发现，a的绝对值越大，抛物线的开口就越小，a的绝对值越小，抛物线的开口就越大。但这毕竟没有具体量化。你知道抛物线的开口大小到底要怎么量化吗？

事实上，抛物线在不同的竖直位置上，开口的大小是不同的。我们对最简单的抛物线y=ax^2 (a>0)做一个探究。它与直线y=y0两个交点的横坐标差，就表示抛物线在y=y0的开口大小。

因此我们得到一个关于x的二次方程：ax^2-y0=0. 显然，此时开口的大小为|x2-x1|=根号(4ay0)/a=2根号(y0/a). 这样我们就可以得到抛物线y=ax^2在不同的竖直位置上的开口大小。比如，在y=1的开口大小是2根号(1/a)，在y=2的开口大小是2根号(2/a)，在y=1/4的开口大小是根号(1/a).

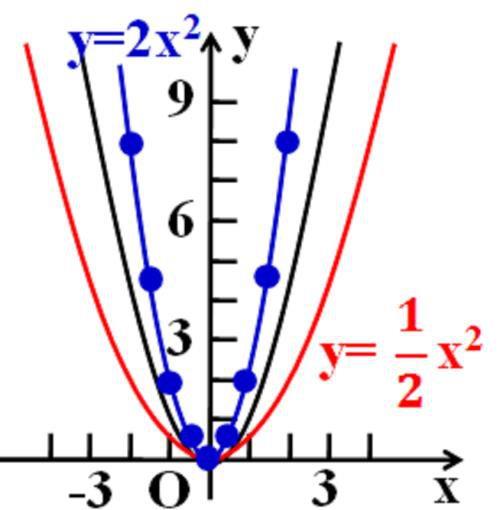
当a值不同时，形成多条抛物线之间的开口对比。比如对比这三条抛物线：y=x^2/2, y=x^2, y=2x^2. 我们可以选择在同一竖直位置上，比较它们开口的大小。比如在y=1/4的竖直位置上。y=x^2/2的开口大小为根号2, y=x^2的开口大小为1，y=2x^2的开口大小为根号(1/2). 很明显的，就可以对较三者之间在y=1/4的开口的量化大小了。

如果我们取y=y0>0，就可以发现，抛物线y=ax^2 (a>0)的开口大小，与a的算术平方根成反比。即a越大，开口就越小。而且可以对其大小进行量化。类似的，我们也可以探究a<0的情形。最终得到结论，抛物线y=ax^2在同一竖直位置上，|a|越大，抛物线开口越小。并且这种大小是可以量化的。

由于抛物线在水平方向上平移，并不会改变抛物线在同一竖直位置上开口的大小，所以顶点式y=a(x-h)^2+k中的参数h并不会影响到上面的结论。而当抛物线在竖直方向上平移时，在同一竖直位置上的开口大小就会发生变化。

为了更好地掌握这种变化的规律。我们选定一个开口大小，比如开口大小等于2时，可以发现，这时a=y0. 也就是说，对于抛物线y=a(x-h)^2，我们要衡量它的开口大小，只需找到它的开口等于2时的纵坐标。此时纵坐标的绝对值越大，说明抛物线的开口越小。

而当抛物线在竖直方向上平移k个单位长度时（k>0向上平移，k<0向下平移）, 抛物线在开口等于2的竖直位置也会随之变化。由原来的y=y0=a, 平移k个单位长度，变成y0=a+k, 从而有a=y0-k。

这样又得到了一个根据开口等于2的纵坐标位置，求参数a的方法。特别的，当抛物线开口等于2的位置在横轴上时，抛物线y=a(x-h)^2在竖直方向上平移了k个单位长度。此时, a=y0-k=-k.

关于抛物线的开口大小量化问题，最多被运用于拱桥问题。如下题：

图中是抛物线形拱桥，当拱顶离水面2m时，水面宽4m. 水面下降1m，水面宽度增加多少？

注意：水面宽就是抛物线开口的大小。拱顶离水面的距离就是竖直的位置。我们以拱顶为原点作如上图的坐标系，就可以发现。当y=-2时, 开口大小为4，可以求当y=-3时，开口的大小。

解：记开口大小为l，由l=2倍根号(y0/a)，可以知道a=4y0/l^2. 因此可以列方程：

-8/16=-12/l^2, 并解得：l=2根号6. 因此，水面宽度增加了(2倍根号6-4)m.

你学会了吗？这个知识在课堂上想要学到，恐怕不容易哦！

本文内容由小莉整理编辑！