从已知出发顺向思维求解某个角的正弦值和余弦值(知道角度求其正弦值)

导语：从已知出发，顺向思维，求解某个角的正弦值（初三阶段）

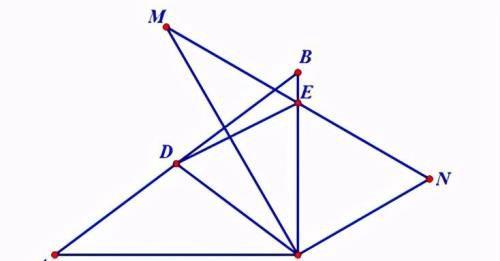
题目：如图，已知Rt△ABC中，∠ACB=90°，AC=8，BC=6，将△ABC绕C点顺时针旋转得到△MNC，点D、E分别是AB、MN的中点，若点E刚好落在BC边上，求sin∠DEC.

思路与分析：

顺向思维：由已知条件出发，逐步向问题靠拢。

题目中显示的已知条件，以及隐含的已知条件（根据显示的已知，不需要大量计算和复杂推理就可以得出的结论）有：

1、BC=CN=6，CA=CM=8（显示）

2、已知直角三角形的两直角边，可以算出斜边，即AB=MN=10（隐含）

3、D、E是直角三角形斜边上的中点，则可以算出CD=CE=5（隐含）

首先看∠DEC是否是特殊角（30°、45°、60°等）。如果是特殊角，则可以直接得出其正弦值。

首先，由两个直角三角形的边长6、8、10看，这两个直角三角形中无特殊角，

而∠DEC=（180°-∠B）/2 （理由：CD=½AB，CE=½MN，故CD=CE，等腰三角形中角的关系），也不是特殊角。

因此，要解sin∠DEC，需要解直角三角形。

过D作DF⊥BC，垂足为F，则我们试着来解直角三角形DEF，如图：

只要求出DF和DE的值，则可以得到sin∠DEF的值。

由DB=DC（理由：CD是直角三角形ABC斜边上的中线）可知，

F是BC的中点（理由：等腰三角形底边上的高），

那么：CF=BF=3（理由：BC=6），

而CE=CD=5（理由：直角三角形斜边上的中线等于斜边的一半）

所以EF=CE-CF=5-3=2

又因为D是AB的中点，F是BC的中点，

所以DF=½AC=4（理由：三角形的中位线）

根据勾股定理，DE=2√5

sin∠DEC=DF/DE，代入DF、DE的值后得sin∠DEC=(2/5)√5

解：

解题过程略。

本文内容由小迪整理编辑！