线段值问题专题方法(线段值问题例题)

通常，我们把直线外一点到这条直线的垂线段的长度叫做点到直线的距离；经过探究我们得到一个事实：直线外一点与直线上各点连接的所有线段中，垂线段最短.

即我们今天所要讲的内容“斜大于直”问题。

“斜大于直”问题在中考线段最值中考察较为广泛，即点到线的最短距离问题，常见的有：

单线段的最值；

线段和的最小；

系数不为1的线段和的最值（胡不归问题）.

二、例题精选

基本模型：点P到直线MN的最短距离为线段PA的长.

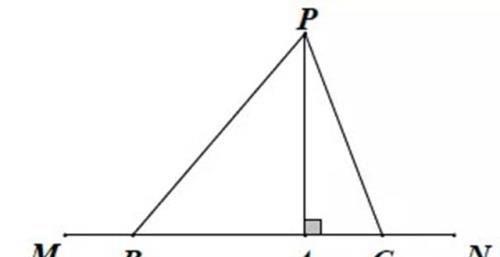
常规题型

点P是Rt△ABC斜边AB上的一点，PE⊥AC于E，PF⊥BC于F，BC=6，AC=8，则线段EF长的最小值为_____.

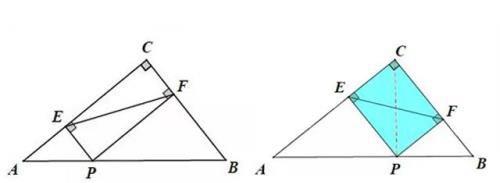
简析：利用矩形的对角线相等，将所求的线段EF转化为PC，再利用垂线段最短（斜大于直）即可知线段PC的最小值为4.8.

变式1：“隐点型”----（对称隐藏定点型）

如图，矩形ABCD中，AB=20，BC=10，点M为对角线AC上一动点，点N为边AB上一动点，连接BM，MN，则BM+MN的最小值为_______

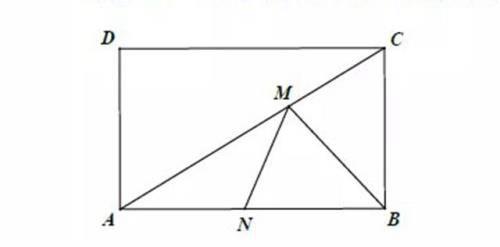
分析：同化异：当动点个数超过1个时，我们解题时习惯先假设其中一动点为定点，如将点N看作定点，则本题为典型的“饮马问题”，即做定点B关于河（动点M所在的直线AC）的对称点即可。

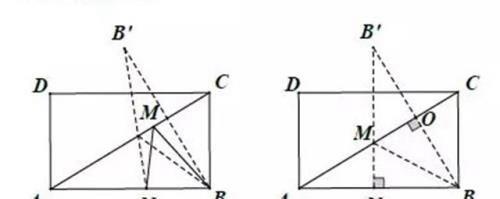
折化直：因点N为动点且在直线AB上运动，则本题转化为定点B’到直线的最短距离，即当B’N⊥AB时最短（斜大于直）.即BM+MN的最小值为线段B’N的长。

变式2：“隐点型”----（运动轨迹隐藏定点型）

如图，AB=√3，点P是线段AB上一个动点，分别以AP，BP为边在线段AB上方做等边△AEP和等边△BFP，连接EF，则△PEF外接圆的半径最小值为_____

解析：要求△PEF外接圆半径的最小值，必须找出三角形的外心所在的位置，因外心为三边垂直平分线的交点，不难发现只要做PE和PF的垂直平分线，交点即为圆心。

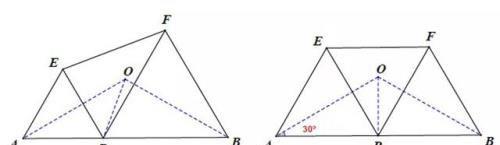
由△AEP和△BFP均为等边三角形可知：PE，PF的垂直平分线即为∠EAP和∠FBP的角平分线，则可知交点O为定点，则根据“线段最短”（斜大于直）可知OP垂直AB时，OP最小，解直角三角形可得最小值为2

反思：

①本题的关键在于确定△PEF的外心，利用等边三角形的特殊性将垂直平分线的交点转化为角平分线的交点，寻找到外心.

②发现外心为一定点，则转化为求定点到直线的最短距离问题，即垂线段最短（斜大于直）.

关于线段最值问题的研究，飞扬老师分为三篇文章讲述，通过18年中考典型例题来探究此类问题的解题思路。欢迎同学们关注下篇文章的例题。

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请与我联系，一经查实立刻删除内容。本文内容由快快网络小萱创作整理编辑！