两条直角边的比值(已知直角两条边怎么算角度)

导语：一道初中几何题-求直角边上的两条线段的比

一道初中几何题-求直角边上的两条线段的比

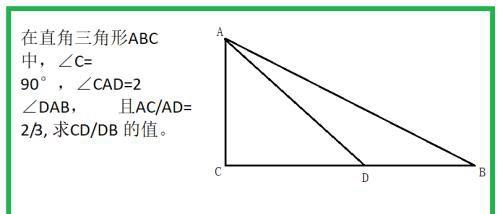
在直角三角形ABC中，∠C=90°，∠CAD=2∠DAB， 且AC/AD=2/3, 求CD/DB 的值。

解法1： 初中解法，如图做角CAB的平分线，交于CD于点P。

由于是计算比值，可以直接把AC看成AC=2， AD=3， 这样不影响结果。

在直角三角形ACD中，根据勾股定理可以直接求得：

CD=√5

根据三角形角平分线定理，可以得出：

CP/PD=AC/AD=2/3,

所以：

CP=2CD/5=(2√5)/5

PD=3CD/5=(3√5)/5

因此在直角三角形ACP中， 斜边AP可以求出：

设BD=x, 那么根据勾股定理：

在三角形PAB中再次用角平分线定理：

将此化简后有：

解这个方程：

所以：

CD/DB=5/9

解法2： 高中解法，利用三角学的恒等变换。

如图， 设∠BAD=θ， 则∠CAD=2θ，∠CAB=3θ，

在直角三角形ACD中， 显然有：

Cos2θ=AC/AD=2/3

其次通过解直角三角形用θ表示可以列出DC和BC的表达式，因此：

通过三角的恒等变换：

可以解出：

利用三角的恒等变换公式：

最后得出：

本文内容由小里整理编辑！