角格点经典例题(角格点问题全解)

平面几何中的“角格点”问题是属于难度类的几何题（大家一般都会推讨其的纯几何求解方法）。其：题意简明却有难度、知识点多颇有技巧。今选经典一例给出三种解法，供参考：

【题】（如图）己知：在正三角形△ABC中，点D为其内一点，且：∠CBD=42º，∠BCD=54º，求：∠CAD的度数

【分析1】造外心.引四点共圆.寻全等导角

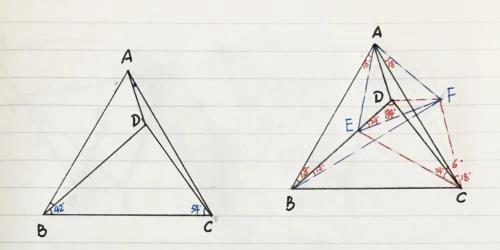
（1）过点C作∠BCA的平分线交BD于点E，连接AE，由已知正△ABC得：EC为边AB的中垂线，∴EA=EB，∠EAB=∠EBA=60º－42º=18º

（2）以AE为边如图作正△AEF，连接BF，则：点E为△ABF的外心，∴∠ABF=∠AEF/2=30º，∴∠EBF=12º=∠EFB，∠DEF=24º

（3）易得∠FAC=18º=∠EAB，FA=EA，AC=AB，∴△ACF≌△ABE，∴∠FCA=∠EBA=18º，∴∠DCF=18º＋6º=24º=∠DEF，∴点D.E.C.F共圆，由∠DCE=30º－6º=24º=∠DCF，∴DE=DF

（4）由上可证：△ADE≌△ADF（sss），∴∠DAE=∠DAF=30º，∴∠CAD=30º－18º=12º

【分析2】利用对称.应用正弦定理.证等腰导角

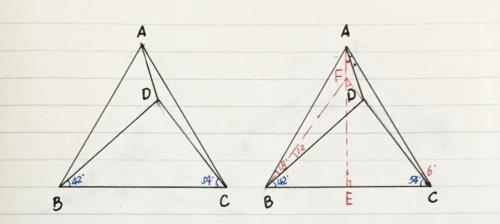
（1）过A作BC边上的高线AE，E为垂足，延长CD交AE于点F，连接FB，则：FB=FC

（2）由己知得∠ABD=18º，∠ACD=6º，易得：∠FBD=12º，∠BFE=∠CFE=36º，∠BDF=96º

（3）在△ACF中，根据正弦定理可得：AF/FC=sin6º/sin30º=2sin6º

（4）在△BDF中，根据正弦定理可得：DF/BF=sin12º/sin96º=sin12º/cos6º=2sin6º，即：DF/BF=DF/FC=2sin6º=AF/FC，∴AF=FD

（5）得∠FAD=36º/2=18º，所以：∠CAD=12º

【分析3】三造等腰梯形.引出三个外心.导角

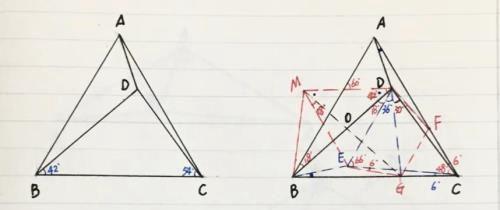
（1）由已知得∠ABD=18º，∠ACD=6º，过点D作AB平行线，过点B作∠ABE=∠BAD成交点E，连CE，即DE∥AB，∠BDE=∠ABD=18º，ABED为等腰梯形，∴AD=BE，∠CAD=∠CBE，易证：△CAD≌△CBE，∴∠BCE=∠ACD=6º，CD=CE，∠DCE=48º，∠CDE=∠CED=66º

（2）在CA上取点F，连FD，使FC=FD，过点F作FG∥DE，交BC于点G，连GE，△CFG为正三角形，易证：△CDF≌△CEG，得∠DEG=72º，连DG，由FC=FG=FD，∴点F为△CDG的外心，∴∠GDC=∠GFC/2=30º，∴∠GDE=36º，在△DEG中计祘得∠DGE=72º=∠DEG，∴DG=DE

（3）以DE为边如图作正△DEM，连MB、MG，由上得：DG=DE=DM，所以：点D为△EMG的外心，∴∠EMG=∠EDG/2=18º=∠EDB，设MG交BD于点O，易证OM=OD，MD∥BG，所以可得MG=BD，∴MBGD为等腰梯形，MB=DG，∴MB=ME=MD，则点M为△BDE的外心，∴∠DBE=60º/2=30º

（4）所以∠CBE=42º－30º=12º，∴∠CAD=12º

以上三个之分析，“道听度说”供参考。

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请与我联系，一经查实立刻删除内容。本文内容由快快网络小媛创作整理编辑！