ad是△abc的中线ef分别在abac上(△abc中ad是bc上的中线说明)

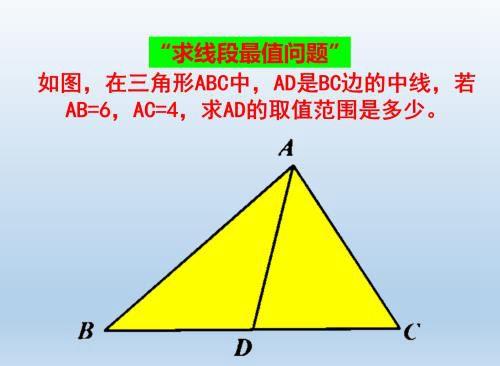
导语：▲ABC中，AD是中线，AB=6，AC=4，求AD的取值范围是多少。

题目：如图，在三角形ABC中，AD是BC边的中线，若AB=6，AC=4，求AD的取值范围是多少。

解法1：如图，延长AD至E，使得DE=AD，易得BE=AC=4，AB-BE<AE<AB+BE,即2<2AD<10,1<AD<5,

解法2：依中线长l公式有：AD＝｛√（AB²＋AC²）·2一BC²｝/2＝（√104一BC²）/2，…①依三角形两边之和大于第三边，两边之差小于第三边有：6-4＜BC＜6＋4，2＜BC＜10，代入①可得：1＜AD＜5。

解法3：BD＝CD＝a，由斯特瓦尔特定理AB²·a+AC²·a-AD²·2a＝2a³，→18+8-AD²＝a²，→.AD²＝26-a²，AB-AC＝2＜2a＜AB+AC＝10，既1＜a＜5，5＝✓25＞AD＞1²＝1

解法4：用中线定理，AB²+AC²=1/2BC²+2AD²AD²=(6²+4²-1/2BC²)/2BC取值范围为(2,10)通过上式计算得出AD的取值范围(1,5)

解法5：用中线定理，AB²+AC²=1/2BC²+2AD²AD²=(6²+4²-1/2BC²)/2，BC取值范围为(2,10)，通过上式计算得出AD的取值范围(1、5)。

本文内容由小畅整理编辑！