代数数论是什么(代数数论知识总结)

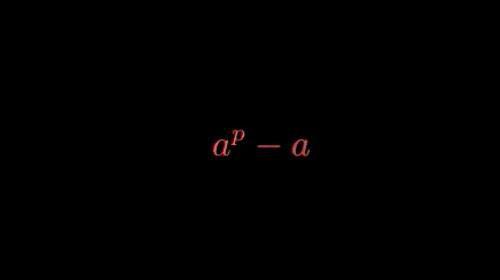
导语：代数数论概念系列文章——引入代数数论的讨论(1)

想写什么？

代数数论为数论的一个分支，代数工具毫无疑问是代数数论的核心工具，素数(元)是代数数论里最耀眼的明星。

笔者不是数学高手，写这一系列的文章，不是用来说教，只想与读者们一起学习探讨。

对数学有兴趣的人很多，但一旦深入一些学数学，很多人便没有兴趣了。很想让数学类的文章有强大的吸引力，男人看了永远18岁，女人看了永远16岁。但这不可能，好比男人不可能永远18岁，女人不可能永远16岁。

想了很久，如何向没有接触过代数数论的读者系统介绍代数数论，且让读者看了文章有所收获，又让文章稍微不是那么无聊呢？或许有办法，努力吧。

代数数论概念系列文章从最基础的代数概念讲起，力求写出概念的内在联系。每一个定理的证明力求不跳过任何重要的步骤，让仅有高中数学能力的人也能看得懂。

引入代数数论的讨论

本文分成两部分，用数论里的两个定理，向读者们展示代数学对数论研究的有力推动，人类智慧的拓展，不要求读者看懂。

本文第一部分叙述费马定理的古典证明与代数证明。

（1）费马定理的古典证明与代数证明

设a为任意整数，p为素数，那么

费马小定理左边表达式

是p的倍数。用数学公式表述为

费马小定理

费马定理一般的表达公式为

a不为p的倍数的费马定理公式

用这个公式表述费马定理的时候，a不为p的倍数。

费马定理有很多种的证明办法，本文所叙述的证明方法非常经典，很容易看懂。

（a）费马定理的古典证明

假设a为正整数(为什么不用考虑a为负数的情况？)，且a不能被p整除，用p除数列

数列

可得余数,这些余数重新排序后构成数列

余数数列

问读者一个小问题，为什么p与a, 2a, 3a, ..., (p-1)a分别相除得到的余数的数量为p-1个呢，且重新排序后组成的数列如图所示呢？

显然有

得到

由此证明了

成立。

（b）费马定理的代数证明(群论)

这种证明方法利用了拉格朗日定理：子群的阶(个数)整除群的阶。

由群论里的群定义可知，所有整数除以p，余数能得到一个整数集

群

该整数集在乘法意义上形成阶为p-1的群，该群称之为p-1阶的循环群。

设a为正整数(同问：为什么不用考虑a为负数的情况？)，p不能整除a，由a除以p会得到一个余数r，且1 ≤ r ≤ (p-1)。那么必有某一个数k为满足

费马定理

的最小正整数，由拉格朗日定理得到kn = p-1(n为正整数)，所以有

令a=pq + r(p为整数)，a的p-1次方与r的p-1次方模p同余，即

同余

原因在于

还有什么......

从而费马定理成立。

有些数论定理用古典方法可以证明，有些定理则无法做到这一点。古典方法能证明费马定理，但无法证明费马大定理。神奇的是，当代代数做到了这一点。

本文的另一部分将讲述代数数论领域的一些定理：素整数在实数域不能表述为其本身与1之外的两个正整数的乘积，但在复数域可以表示为两个高斯素数的乘积，这一陈述有着深刻的代数背景。

本文内容由小故整理编辑！