高中物理等效思想(高中物理等效替代的思想有哪些)

导语：高中物理必修第二册-等效思维(分解与合成)—在曲线运动中的应用

等效思维(分解与合成思想)——在曲线运动问题中的应用(二)

1．概述

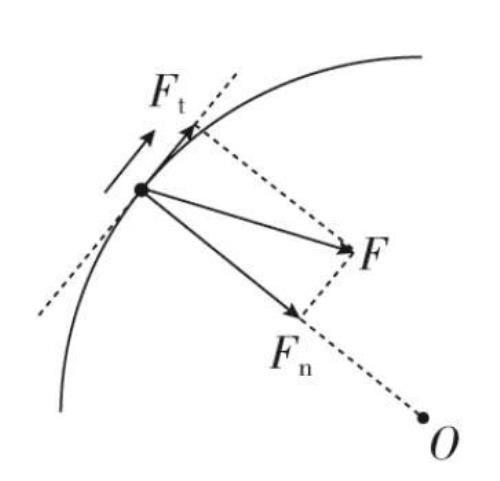
第五章讲述了建立固定的直角坐标系分解曲线运动的方法，其特点是两个分运动均为直线运动，可以用直线运动的规律分析求解。除此之外还有一种较常用的分解曲线运动的方法，即不分解位移、速度，而只将力或加速度按运动的切向和径向方向进行分解。

这种分解方法常用于涉及变速圆周的向心力、速率变化问题，也可用于一般曲线运动(此时可借助曲率半径的概念和圆周运动的规律分析)。其一般步骤为：

(1)将力分解为切向力Ft和径向力Fn；

(2)在沿轨迹切线方向运用牛顿运动定律和加速度的定义分析计算，在沿垂直轨迹切线方向运用向心力公式和圆周运动规律分析计算；

(3)运用矢量合成法则综合得出合运动的规律。

2．两种分解方法的比较

(1)按运动的切向和径向方向对曲线运动进行分解，实际是在运动轨迹的某一点建立与该点速度方向有关的直角坐标系(即移动直角坐标系)，只能分析该点附近的短暂瞬时运动过程。这种方法只适于某一点的瞬时值分析计算，常用于定性分析变速圆周运动的整个过程。

(2)沿固定方向建立直角坐标系对曲线运动进行分解，优点是可以用直线运动的规律定量分析求解，常用于除圆周运动之外的一般曲线运动，应用更普遍。

值得注意的是：物体做变速圆周运动时，一般按切向和径向方向进行分解分析，需要注意物体沿垂直于运动方向受力不平衡，且物体所受的合力既不等于径向合力，也不等于切向合力。

本文内容由小媛整理编辑！