自然数的产生和发展(自然数的由来与发展)

导语：“有温度的数学”——自然数的形成与发展（进位制与位值制）

自然数的表示方法——进位制与位值制

随着生产实践的进一步发展，人类需要计数更大的数目，这时就必须将记数的方法系统化，否则无法表示大数目。在人类发展史上，曾经出现过多种记数方法（有不同的进位制，但都没有位值制，一直到印度——阿拉伯计数系统的出现）。

①数基（或者&34;）。

在历史上，曾经出现过以2、3、4为原始的数基，但比较多的还是以5、10、20、60为数基，即五进制、十进制、二十进制、六十进制。最多的是以10为数基，即现在世界各国通用的十进制，亦即&34;的方法。当然，在计算机时代，二进制也发挥了巨大的作用。

②位值制。

由于人共有10根手指，所以产生十进制并不为奇。在古代文明中，世界各国大多数都是采用的十进制，例如中国、罗马等。但十进位记数法，离十进位值制还有关键的一步要走，即&34;简称&34;。所谓&34;，是指相同的记数符号由于所处的位置的不同而可以表示大小不同的数目。举一个简单的例子，1231，这个数出现了两个数字1，但一个代表1，另一个代表1000.由于有了位值制，就可以用有限个数字表示出无限多个自然数，这是记数史上的一个创造，一个奇迹。因此，马克思在他的《数学手稿》一书中称十进位值制记数法为&34;。

图（7—2）

&34;的发明要比&34;晚得多，因此在小学数学的自然数概念教学中，理解&34;是非常抽象的。教学中要根据学生已有的经验（例如会说数的名称，数数的活动）并借助于&34;、计数器、或者算盘等形象的记数材料，设计有趣的数学活动来深刻理解&34;的概念。

③中国古代数学的贡献——算筹与筹算

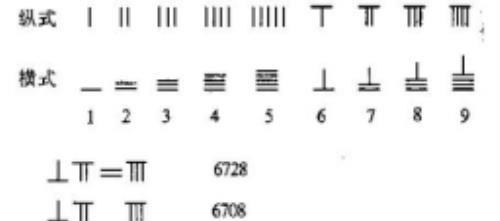
中国古代是用算筹表示数字的，如下图所示：

为什么要用纵式和横式两种不同的摆法呢？这就是因为位值制的需要。算筹记数的表示方法为：个位用纵式、十位用横式、百位再用纵式、千位再用横式、万位再用纵式……这样从右到左，纵横相间，以此类推，就可以用算筹表示任意大的自然数。

由于位与位之间的纵横变换，且每一位都有固定的摆法，所以既不会混淆也不会错位。运用算筹进行四则运算（就是筹算），就非常方便快捷。

中国古代算筹记数法在世界数学史上是一个伟大的创造。把它与世界其它古老民族的记数法作一比较，其优越性是显而易见的：古罗马的数字系统没有位值制，只有七个基本符号，要记稍微大一点的数就非常繁难。古美洲玛雅人虽然懂得位值制，但用的是20进位，古巴比伦人虽然懂得位值制，但用的是60进位。20进位至少要用19个数码，60进位要用59个数码，这就使记数和运算变得非常复杂，远不如只用9个数码便可以表示任意自然数的十进制来得简捷方便。

但中国的算筹记数也有一大缺点就是没有表示&34;的算筹（另外，它不是用符号表示的，没有&34;表示也是中国数学的一大缺点），若表示&34;时，就用&34;，实际上在进行算筹计算时容易混淆。直到印度人发明了数码&34;，十进制的印度——阿拉伯数系才是当前最完备的记数系统。

小数点儿说：了解了进位制与位值制的发展和历史形成过程，才能感受到课堂教学中位值观念的建立给孩子心中种下了一颗多么神奇的数学的种子，我们在教学过程中更加够敬畏尊重这部分知识，并正确看待孩子学习过程中出现的错误，更能探索怎样去构建进位制与位值制。

本文内容由小思整理编辑！