等效思想在高中物理中的应用(等效思维方法及其运用)

导语：利用“等效思维”解决物理问题----“运动的合成和分解”灵活应用

在中学阶段，我们学习过的最基础的三大运动是匀速直线运动、匀变速直线运动、匀速圆周运动。其他很多复杂的运动都可看成是同时参与这三种运动中两种不同运动而形成的。因此，在研究物体做比较复杂运动时，可以利用“运动的合成和分解”方法把其分解为两个简单的运动来研究。这就是采用“等效思维”把不熟悉复杂的问题转化成熟悉简单的问题研究，换个角度看问题，一切变得清晰可见。这正好体现是高考能力要求。

一.把物体运动分解为两个分运动的方法。

1. 根据物体运动的实际效果来分解。

如小船过河时，小船沿船头划行的同时随水流运动，其实际运动可分解为船头方向和水流方向两个分运动来研究。

2. 把物体运动分解在互相垂直的两个方向上。（正交分解法）

如物体做平抛运动时，可分解为水平方向的匀速直线运动和竖直方向的自由落体运动来研究；物体做斜上抛运动时，可分解为水平方向的匀速直线运动和竖直方向的竖直上抛运动来研究。

3. 沿物体运动的初速度方向和所受合外力方向分解。

如研究礼花炮升到最高点爆炸后各小部分向四周飞出去的运动时，可把各小部分的运动分解为其初速度方向的匀速直线运动和竖直方向的自由落体研究。很容易知道爆炸后各小部分在一个球面上扩张，整体自由下落。

二. 物体的合运动和同时参与的两个分运动间的关系。

1. 等效性：物体同时参与两个分运动的实际运动就是合运动。

2. 独立性：物体同时参与的两个分运动间互不干扰、各自独立。

3. 等时性：物体参与的两个分运动和合运动同时开始、同时结束。

4. 矢量性：物体参与的两个分运动和合运动，它们间的位移、速度、加速度遵循平行四边形定则。

三. 利用“运动合成和分解”解决问题的步骤。

1. 根据物理情景和研究的问题，选择相应的方法把物体的实际运动分解成两个分运动。

2. 根据平行四边形定则，作出物体运动到某一特殊位置时，其合运动和两分运动间的速度矢量图（或位移矢量图、加速度矢量图）。

3. 根据已知条件和求解问题，理清解题思路并列方程求解。

四. 利用“运动合成和分解”解决问题集锦。

例1：有一条两岸平直、河水均匀流动、流速恒为v的大河.小明驾着小船渡河，去程时船头指向始终与河岸垂直，回程时行驶路线与河岸垂直.去程与回程所用时间的比值为k，船在静水中的速度大小相同，则小船在静水中的速度大小为(　　)

A. B.

C. D.

答案　B

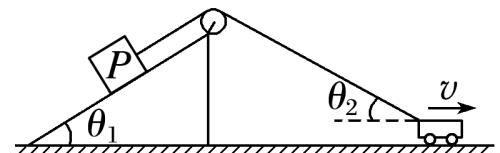
例2：质量为m的物体P置于倾角为的固定光滑斜面上，轻细绳跨过光滑轻质定滑轮分别连接着P与小车，P与滑轮间的细绳平行于斜面，小车以速率v水平向右做匀速直线运动，重力加速度为g.当小车与滑轮间的细绳和水平方向的夹角为时如图所示，下列判断正确的是(　　)

A.P的速率为v

B.P的速率为

C.绳的拉力等于

D.绳的拉力小于

答案　B

例3: 如图所示，B为竖直圆轨道的左端点，它和圆心O的连线与竖直方向的夹角为α.一小球在圆轨道左侧的A点以速度平抛，恰好沿B点的切线方向进入圆轨道.已知重力加速度为g，不计空气阻力，则A、B之间的水平距离为(　　)

A. B.

C. ​ D.

答案　A

例4：甲、乙两个同学打乒乓球，某次动作中，甲同学持拍的拍面与水平方向成角，乙同学持拍的拍面与水平方向成角，如图所示.设乒乓球击打拍面时速度方向与拍面垂直，且乒乓球每次击打球拍前、后的速度大小相等，不计空气阻力，则乒乓球击打甲的球拍的速度大小与乒乓球击打乙的球拍的速度大小的比值为(　　)

A. B. C. ​​ D.

答案　C

例5：如图所示，圆心为O、半径为R的圆形区域内有一个匀强电场，场强大小为E、方向与圆所在的面平行．PQ为圆的一条直径，与场强方向的夹角θ＝.质量为m、电荷量为＋q的粒子从P点以某一初速度沿垂直于场强的方向射入电场，不计粒子重力．

(1)若粒子到达Q点，求粒子在P点的初速度大小.

(2)若粒子在P点的初速度大小在0～之间连续可调，则粒子到达圆弧上哪个点电势能变化最大？求出电势能变化的最大值ΔEp.

答案　(1)　(2)圆弧上最低点

解析　(1)粒子做类平抛运动，可分解为水平方向的匀速运动和竖直方向的匀加速运动研究。

则水平方向有：

竖直方向有：

由牛顿第二定律得qE＝ma

联立解得

(2)粒子到达圆弧上最低点电势能变化最大

解得

例6：如图所示，在磁场方向水平向右的匀强磁场中，一带正电粒子以速速进入磁场，速度与磁场方夹角为θ，带电粒子将做螺旋运动，试求带电粒子做螺旋线运动轨迹的横截面半径r和螺距h大小。

答案： ,

解析：带电粒子的螺旋运动可分解为在垂直磁场方向的平面内做匀速圆周运动和沿磁场方向做匀速直线运动来研究，如图所示。

由几何关系可知： ，

在垂直磁场平面内带电粒子做匀速圆周运动： ， 解得

带电粒子转动一周时间： ， 解得

在沿磁场方向带电粒子做匀速直线运动： ， 解得 。

例7：如图所示，空间中存在着水平向右的匀强电场，电场强度大小 N/C，同时存在着水平方向的匀强磁场，其方向与电场方向垂直，磁感应强度大小B＝0.5 T．有一带正电的小球，质量 ，电荷量，正以速度v在图示的竖直面内做匀速直线运动，当经过P点时撤掉磁场(不考虑磁场消失引起的电磁感应现象)，取.求：

(1)小球做匀速直线运动的速度v的大小和方向；

(2)从撤掉磁场到小球再次穿过P点所在的这条电场线经历的时间t.

答案　(1)20 m/s　方向与电场方向成60°角斜向上 (2) s

解析　(1)小球做匀速直线运动时受力如图甲，

其所受三个力的合力为零，有 得v＝20 m/s

速度v的方向与电场E的方向之间的夹角为θ，则，得 θ＝60°

(2)解法一　撤去磁场后小球做曲线运动，如图乙所示，可分解为初速度方向的匀速运动和合力方向的匀加速运动研究。

其加速度为

小球在初速度方向上的位移为x＝vt

小球在合力方向上的位移为

小球再次穿过P点满足

联立解得

解法二　撤去磁场后小球做曲线运动，可分解为水平方向的匀加速运动和竖直方向的竖直上抛运动研究。

小球在竖直方向上其初速度为

当小球再次穿过P点所在的电场线时，，其在竖直方向上的位移为零，则

联立解得.

本文内容由小荣整理编辑！