新高考数学解答题题型(高考数学题新高考)

导语：新高考政策下，数学题到底怎样解才能更好的拿高分

你品，你细品这道数学压轴题，这是一道很值得品味的考题。今天组合教育小合来和同学们聊聊高考数学压轴般的题目，我们一起来挑战高考数学的不同解题思路。

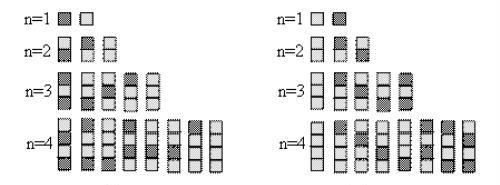
题目：给N个自上而下相连的正方形着黑色或白色。当N≤4时，在所有不同的着色方案中，黑色正方形互不相连的着色方案如下图所示：

高考数学题

这道题图文并茂、能力立意、新旧融合、背景新颖厚重、渗透课改理念，重点考查学生阅读理解能力、分析问题和解决问题的能力，考查分类讨论思想、合情推理能力和数学素养。

同学们可以发现，当N=6时，黑色正方形互不相连的着色方案共有种，至少有两个黑色正方形相连的着色方案共有21种。

本题图文并茂信息量大，信息的选择直接影响解题方向。题目中给出的当N≤4时，黑色正方形互不相连的着色方案的4组图形信息，看是可有可无好象只是用来帮助考生理解题意的，其实不然，这四组图形信息才是本命题的最大亮点，若去掉这一图形信息该命题则黯然失色命题效果则大打折扣。

小合则认为给出的四组图形的结构不尽合理，不符合分类讨论由易到难由简到繁循序渐进的认知规律，特别是N=4时的着色方案图给人分类混乱之感。若将给出的四组图换成图2的结构形式，更能帮助考生理解题意，这样命题就更加完美了，这不能不说是本命题的一个小小的瑕疵，当然瑕不掩瑜。

如果认为图形信息只是用来帮助理解题意，可得如下解法1，若将四组图形当作是四个特例，作为归纳的起点可得如下解法2。可见这一图形信息不仅用来帮助理解题意，而且给考生提供了更多的思维空间，给考生创造性地简捷有效地解决问题提供了平台。

解法1:去掉四组图形信息后本题即为：给6个自上而下相连的正方形着黑色或白色，黑色正方形互不相连的着色方案共有多少种，至少有两个黑色正方形相连的着色方案共有21种。

本题是大纲教材和新课标的一个很好对接的案例。解法1是大纲教材的缩影，解法2正是新课标合情推理的要求。解法2以图形为依托，构造数列，通过观察分析进行归纳推理或联想发现规律，从而使问题得以解决。

归纳推理是一种合情推理，归纳推理从形式上看，是由部分到整体、个别到一般的推理。应用归纳推理可以发现新事实，获得新结论。

法国数学家拉普拉斯曾经说过：“即使在数学里，发现真理的主要工具也是归纳和类比。”随着新课改的不断深入，新课标高考不仅考归纳推理还会考类比推理，事实上类比推理出现在高考卷上已不是什么新鲜事了，类比推理与归纳推理相比，类比推理更富创造性和开拓性，同样会成为高考的亮点。

组合教育近期推出的高考数学小题保分班，专门整理了10套解题方法，主要解决学生平时复习遇到的3大难题：做题慢、没思路 、考试发挥失常。这些方法可以帮助学生在二轮复习时，将一轮学习的数学基础知识转化为得分能力。

组合教育小题保分班课程大纲

数学结论、证明思路的发现，主要靠合情推理，因此我们不仅要教学生学会证明，也要教学生学会猜想。

本文内容由小碧整理编辑！