晶体的外延生长(晶体外延生长有几种方法)

导语：田口设计案例-晶体外延层生长实验

案例背景

生产集成电路(IC)器件的一个初始步骤是在抛光的硅晶片上产生一个外延层，镶在一个称为感应器的六面柱体上(每面有两块晶片)，这个六面柱体在一个钟形容器里旋转，这个容器通过其顶部的喷咀喷入化学蒸汽并加热。这个过程持续到外延层生长到所要求的厚度，厚度的目标值14.5微米(um)，其误差范围为14.5土0.5微米，即实际的厚度应该尽可能接近14.5，并在区间[14,15]内。当前的设置造成的偏差超过了指定的1.0微米，于是试验人员需要找出可以设置的过程因子使得外延层的不均匀性达到最小，同时确保平均厚度尽可能接近目标值。

稳健参数设计

响应变差可以通过减小噪声变差来减小，但这可能要付出高的经济代价。由Genichi Taguchi最先提出的稳健参数设计(robust parameter design)是一种可选择的策略，该策略是通过探索控制因子与噪声因子间的交互效应来改变控制因子的水平组合来减小响应变差。因为控制因子通常很易于改变，所以稳健参数设计比直接减小噪声变差更经济更方便。

外延层生长试验的因子和水平

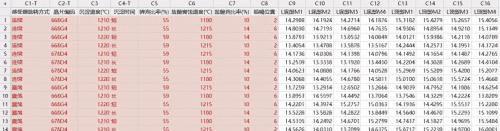
原始外延层生长试验的试验因子如下表所示，共有八个控制因子(A-H)和两个噪声因子(L和M)。

控制因子

低水平

高水平

A. 感受器旋转方式

连续

震荡

B. 晶片编码

668G4

678D4

C. 沉淀温度(℃)

1210

1220

D. 沉淀时间

短

长

E. 砷流比率(%)

F. 盐酸腐蚀温度(℃)

1180

1215

G. 盐酸流比率(%)

H. 喷嘴位置

每个感受器有四个面，因此因子M有四水平。在每一个面上位置幽分顶部和底部(因子L)。在最初的试验中， Kackar and Shoemaber (1986)报告六个面的结果．为了方便说明，这里我们只考虑四个面。因为所期望的是在任何面和位置上都有均匀的厚度，所以因子L和M都处理为噪声因子。

噪声因子

低水平

高水平

L. 位置

底部

顶部

M. 面

1，2，3，4

厚度的目标值是14.5微米，规定误差限制在14.5士0.5微米。这样，试验的目标就是在保持14.5微米的平均厚度的同时，最小化外延层在四个面以及顶、底部上厚度的不均匀性。

乘积表分析

此田口设计的内表采用L16 (2^8)的正交表（表示设计有16个实验和8个因子，以及每个因子2个水平）。外表对两个噪声因子选用了2x4设计，这样每个控制因子水平组合就有8个观测值。那么，按照乘积表分析的话就有16x8=128次实验。

Minitab中田口分析

望目特征问题的两步程序：

选择散度因子的水平使散度最小化（信噪比最大化）

选择调节因子的水平使位置达到目标值

要想第一步中信噪比最大化，则应该取因子组合为：

A1B1C1D1E2F2G2H2

基于以上最佳信噪比组合，预测均值是否达到目标值14.5微米。

由以上预测结果可知，均值没有达到14.5微米，需要进行调节。

从下面的均值主效应图中可以发现，砷流比率(%)是一个合适的调节因子。

为此，我们固定A1B1C1D1F2G2H2，改变E的水平进行预测，结果如下：

根据预测的结果，我们下一步将会固定A1B1C1D1F2G2H2，因子E砷流比率(%)在(55,59)范围内选取，再次进行新的实验。

思考

在本案例中为了实现稳健参数设计，我们用的是田口设计中的乘积表，但乘积表实验次数太多了（128次），有没有其他方法也可以实现稳健参数设计呢？另外，乘积表分析除了实验次数多以外，还有没有其他一些缺点呢？

本文内容由小樊整理编辑！