求三角形面积比例问题(关于求三角形面积的典型例题)

导语：一道初中几何题-求三角形的面积之比的问题

一道初中几何题-求三角形的面积之比的问题

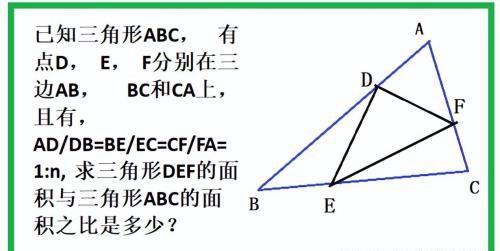
已知三角形ABC， 有点D， E， F分别在三边AB， BC和CA上， 且有，

AD/DB=BE/EC=CF/FA=1:n, 求三角形DEF的面积与三角形ABC的面积之比是多少？

解：根据这种比例关系，可以证明三角形DEF周边的三个小三角形的面积是相等的， 这是因为相邻两边的乘积与其夹角的正弦是相等的， 这点可以通过这样的一个引理得到证明。

引理：共用三角形的一个角的两个夹边的两个三角形的面积之比， 等于其夹边乘积之比。

如图所示：

三角形DBE的面积：三角形ABC的面积=（BD·BE）/(BA·BC),

这个定理用三角形的面积公式=(absinA)/2, 很容易证得。

如果设AB=c, BC=a,

那么：

三角形BDE的面积：三角形ABC的面积=cn/(n+1）·1/a(n+1)ab/ac=n/(n+1)/(n+1)

同理三角形CEF和三角形ADF的面积与三角ABC的面积之比也是n/(n+1)/(n+1)

因此三角形DEF的面积=三角形ABC的面积减去周边的三个三角形的面积，若把三角形的面积看为1， 则三角形DEF的面积为：

3n/(n+1)/(n+1)=（n.n-n+1）/(n+1)(n+1)

即为：

本文内容由小悦整理编辑！