什么是正方形弦图(正方形定理)

导语：正方形弦图几何题5例

在学习弦图内容时，有时会遇到标准弦图，有时我们需要构造弦图来解题，下面介绍5例。

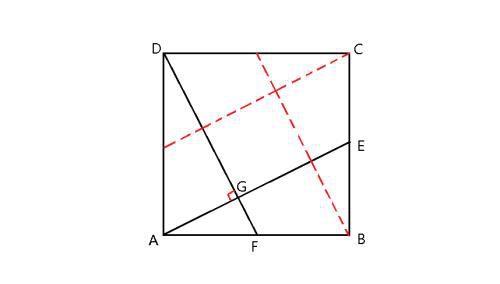
题目1：如下图，在正方形ABCD中，F为AB的中点，连接DF，过A点作DF垂线交DF于G，交CB于E点，GE=3，求正方形的边长是多少？

根据弦图性质，DF⊥AE，F为AB中点，E亦为CB的中点。由该弦图中一些线段的固定比例关系（详见正方形弦图的几个小知识点），GE占AE的3/5,故AE=5。

设EB=X，AB=2X，根据勾股定理得出正方形边长为2√5。

题目2：如图1，等腰RtΔABC中，∠ACB=90°，D是AB上的一点，E是BC上的一点，AE交CD于M，AM=2CM，N是AB的中点，MN=2，若AE⊥CD，求DM的长度？

解题思路：根据弦图性质，将图1补成完整弦图（图2），已知AM/CM=2/1,可知CB/BE=2/1,E点为正方形边长的中点。再根据弦图中的一些线段比例进行计算（详见）

小正方形对角线长2MN=4，边长MF=2√2，占CE长的2/5,CE=5√2。

在大正方形中，BD占对角线AB的1/3,故DE占CE的1/3,CM占CE的2/5。

DM=CE（1-1/3-2/5）=5√2x 4/15=4/3√2 。

题目3：如图，四个完全一样的直角三角形和一个小正方形拼成一个大正方，小正方形面积是1平方米，大正方形面积是5平方米，那么直角三角形中，最短的直角边长度是（1）米。

解题思路：设最短边GD=AF=X，S△AGD=（5-1）/4=1=X(X+1)/2, 最短的直角边X为1。

题目4：如图，在正方形ABCD内，∠AFB=∠CED=90°，AF=CE，连接EF，若EF=3√2，两块阴影部分的面积和为4，则正方形ABCD的面积为（17）。

解题思路：S正方形ABCD-2S△MEF=4S△ABF。

S正方形ABCD=4S△ABF+2S△MEF=4x2+2x3x3x1/2=17。

题目5：如图，已知正方形ABCD的边长为5，点E、F分别在AD、DC上，AE=DF=2，BE与AF相交于点G，点H为BF的中点，连接GH，则GH的长为（√34 /2）。

解题思路：本题重点是证明BE⊥AF（详见上图）。

本文内容由小涵整理编辑！