函数区间值怎么求(求函数区间内大小值)

很多初中毕业生，刚刚开始学高中数学的时候，经常用初中的思维解答问题，出错率就会很高很高。

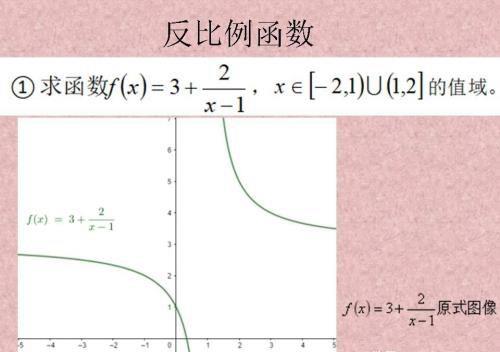
第一、反比例函数，首先要学会反比例函数画图，画出来的图像是双曲线。

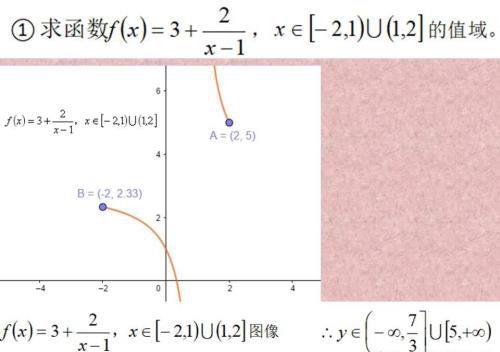
由图像可知，函数图像是断点的，左边的双曲线是有最大值，右边的双曲线有最小值。

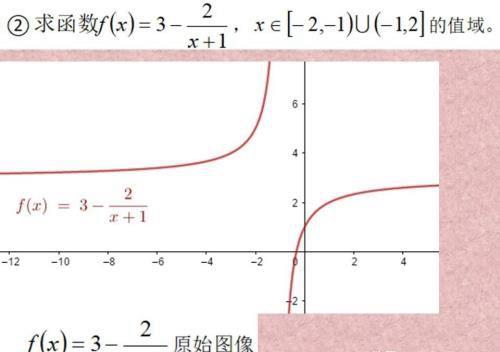
如果产生负号的话，就会产生2,4，象限的情况。

由图像可知，左边的双曲线有最小值，右边的双曲线有最大值。

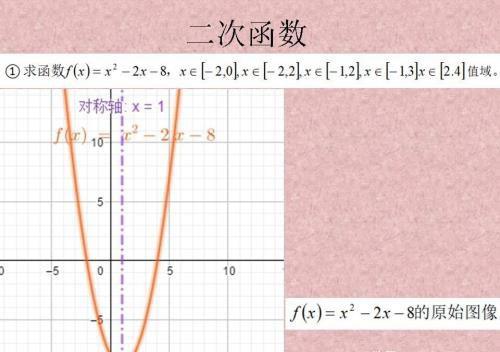
考试的比较多的是二次函数。

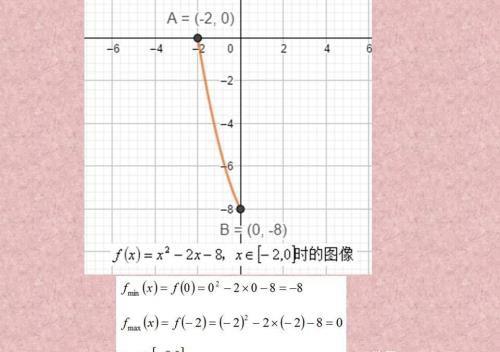
在这个区间的情况下是单调递减函数，比较简单。

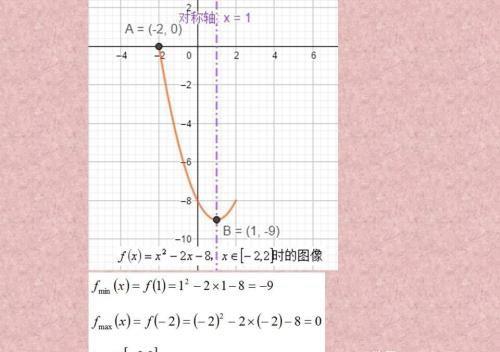
在这种情况下是过了对称轴的情况，最小值在对称轴处取到，最大值在离对称轴比较远的地方取到。

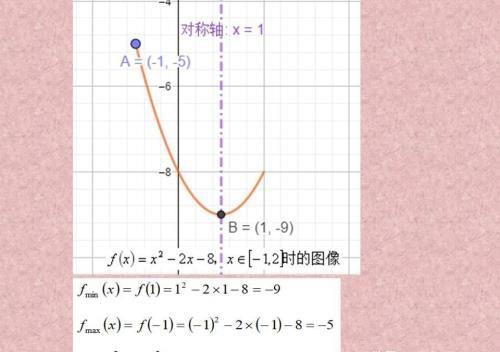
在这种情况下是过了对称轴的情况，最小值在对称轴处取到，最大值在离对称轴比较远的地方取到。

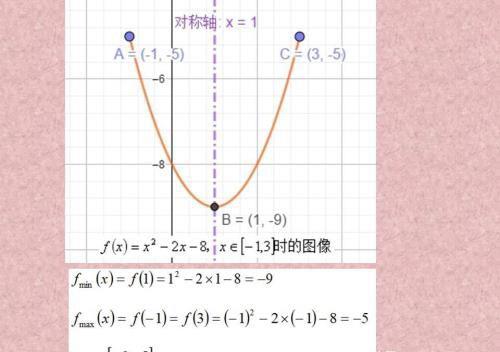
这种情况下，最小值在对称轴处取到，最大值由于是关于对称轴对称的，所以最大值可以在两个端点处取到。

在这个区间的情况下是单调递增函数，比较简单。

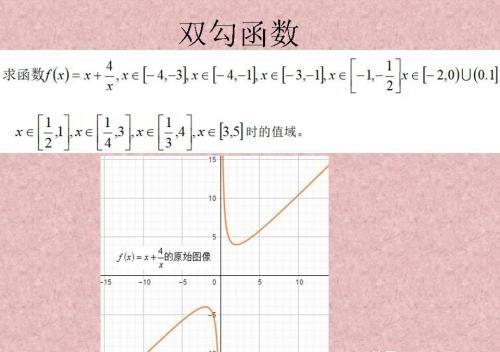
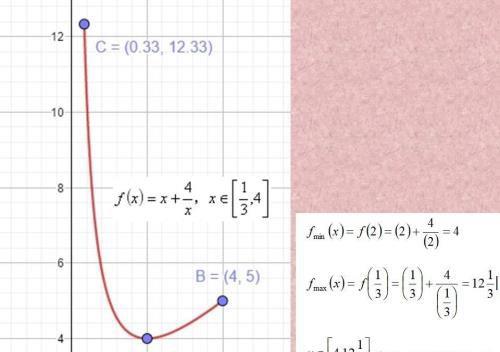
双勾函数是高中的重点函数，要细细的品味哦！（关于原点对称，还有单调性变化）

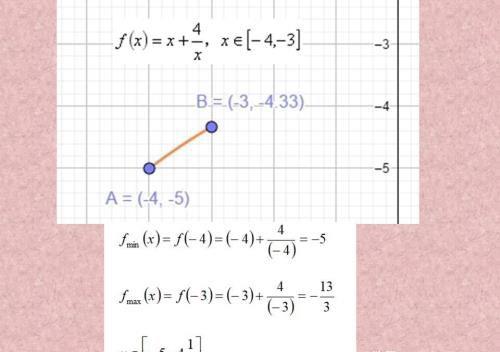
在这个区间的情况下是单调递增函数，比较简单。

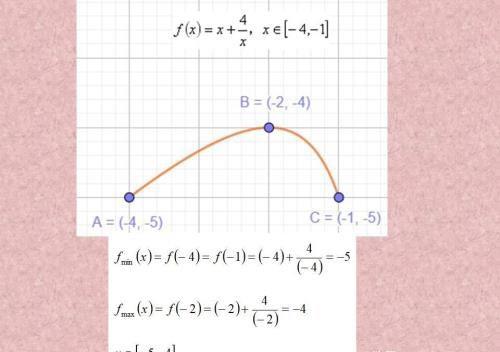
在这个情况下，最大值在-2处取到，最小值在A,C处取到，但是不是关于-2对称哦！

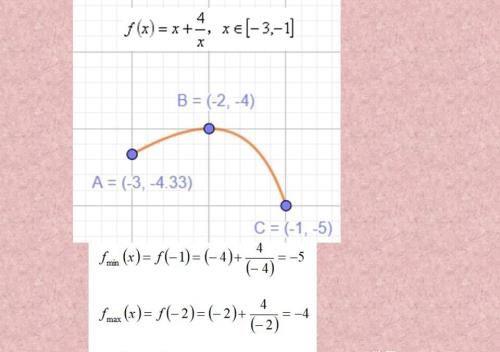
观察图像可知，最大值还是在-2处取到，最小值早C出取到，要带入检验计算才知道哦！

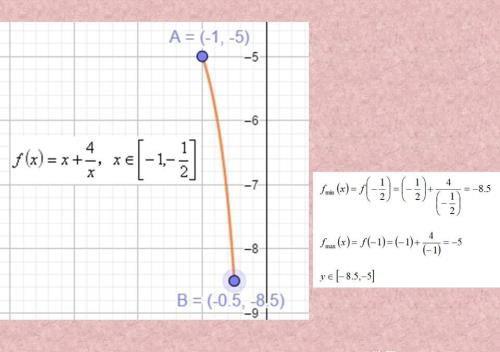
在这个区间的情况下是单调递减函数，比较简单。

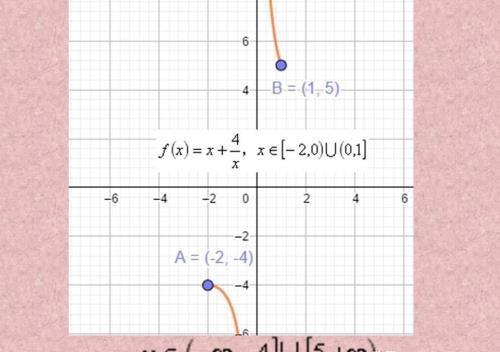
这种情况下分段了，要好好看图像分析，左边取到最大值，右边段取到最小值。

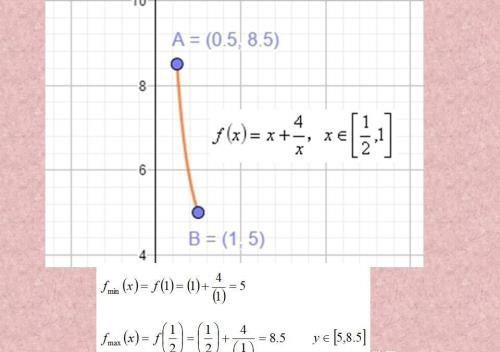
在这个区间的情况下是单调递减函数，比较简单。

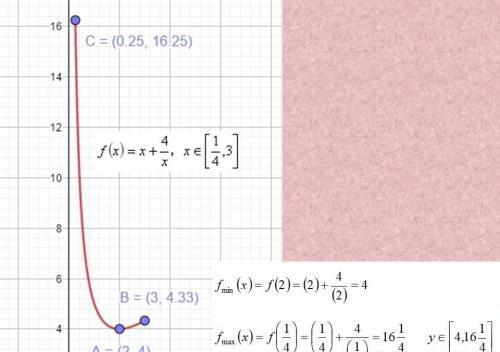
在这种情况下，有增又有减，要细心检验分析得值。

在这种情况下，有增又有减，要细心检验分析得值。

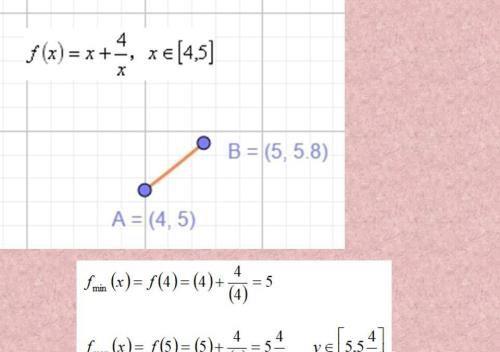
在这个区间的情况下是单调递增函数，比较简单。

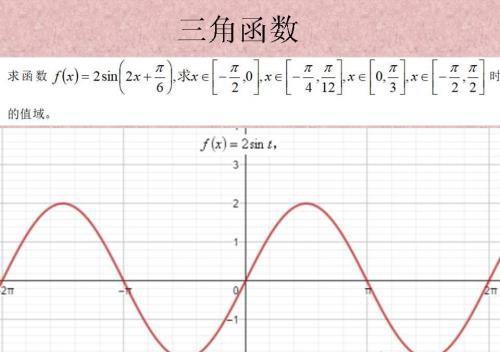
三角函数有波浪，所以考虑起来情况比较多。

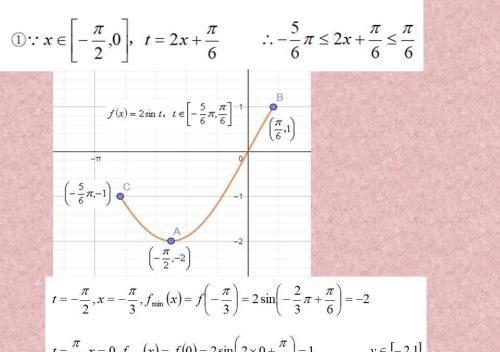
要把t=2x+π/6当做一个整体，再来看函数图像分析，这种带勾的前面已经有了很多，不用怕的。三角函数还是对称的，比双钩简单。

换元之后，只有函数的单调递增，比较简单。

换元之后，图像任然对称，所以有最大值，最小值为两个端点处取到。

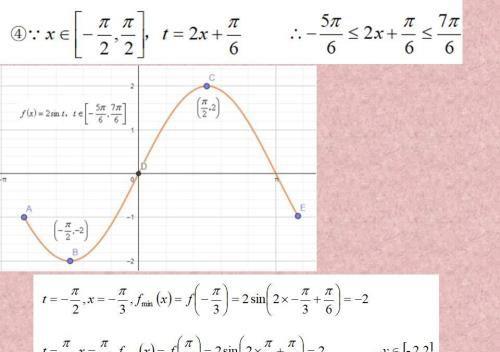
换元之后，还是有波浪线，所以要具体问题，具体分析。

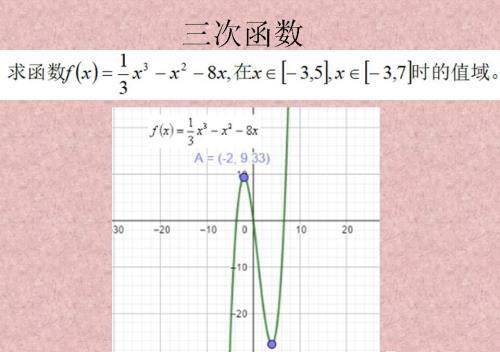
三次函数，一般是这样的情况比较多，相当于有一个最大值，最小值。

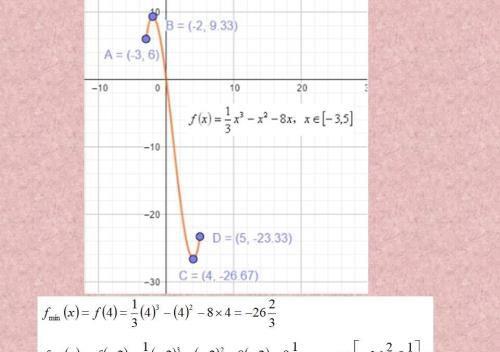
三次函数，区间内求最值。要有图像分析，看得到最大值最小值，要代值检验。

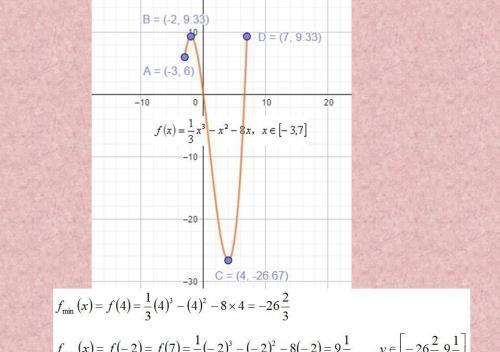
三次函数，区间内求最值。要有图像分析，看得到最大值最小值，要代值检验，对图像有感觉。

高中理科入门点评：区间内求最值的题目，主要的难度在于画图像分析，很多同学做题不愿意画图像，只想直接代值计算，在高中时不行的，在高中一定要学会数形结合，不能偷懒哦！！！

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请与我联系，一经查实立刻删除内容。本文内容由快快网络小璎创作整理编辑！