证明3个连续自然数的积能被3整除(如何证明三个连续的数是3的倍数)

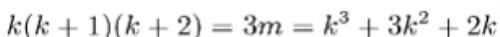
导语：一道高中题-证明连续的三个自然数的乘积是6的倍数

一道高中题-证明连续的三个自然数的乘积是6的倍数

证明n(n+1)(n+2)被6整除，n是自然数，n≥1.

证：利用归纳法，参见数学归纳法原理和例题原理。

第一步：验证初始的时候结论是正确的

当n=1的时候，

显然n(n+1)(n+2)=1x2x3=6, 因此原式是被6整除在n=1是成立的。

第二步：假定n=k的时候是正确的

假定n=k的时候，n(n+1)(n+2)被6整除，k是自然数，

由于连续的三个自然数的一定有一个偶数，即它们的乘积能被2整除，这样我们只要假定

k(k+1)(k+2)=3m, 其中m是自然数，

左侧展开后为：

第三步：证明n=k+1结论是正确的

将n=k+1带入原式，

稍微将上面右侧的等式整理一下让其出现步骤2的形式，然后把步骤2中的结果带入上述式子，

这表明当n=k+1的时候，原式是能被3整除的，同时因为三个连续自然数的乘积一定是个偶数，因此当n=k+1的时候，n(n+1)(n+2)也是被6整除的，至此完成归纳法的证明。

本文内容由快快网络小涵创作整理编辑！