递归算法求大值的复杂度(如何用递归求大值)

导语：递归算法求最大值

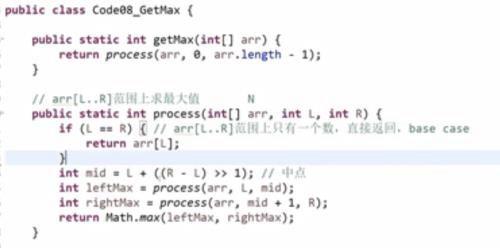
求数组中的最大值

该函数的功能是 在L和R范围上返回最大值

1、 L=R表示就一个数 最大值是它自己

2、如果不止一个数 就求中点的位置

一般的写法是 (L+R)/2

但这些写有问题 如果数组长度很大 L+R可能会溢出

溢出之后 结果可能为负值

可以写成 L + (R-L)/2

(R-L)/2 表示 L ～ R 之间距离的一半

L 加上 一半的距离 也是 L ~ R 的中点

这个结果是不溢出的 因为 L、R都不溢出，R>L，所以R-L也不溢出

更简洁的写法

L + （(R-L)>>1） 右移一位 就等同于除2了

右移一位比除2要快

3、L ～ mid 范围的调用递归求一个左侧部分的最大值

4、mid+1 ～ R 范围的调用递归求一个右侧部分的最大值

5、全局最大值就是左侧最大值和右侧最大值较大的那个

举例

p（0，5）

中点位置是5/2=2的位置

p(0,2）是0~2范围上求个最大值

p(3,5)是3~5范围上求个最大值

只有都返回结果了

才知道0～5范围上的最大值是谁

p(0,2)又分为p(0,1)和p(2,2)

p（2，2）就是它自己了 直接返回

以此类推 递推函数的依赖图如下

所有的子点跑完

最终汇总到p(0,5)的时候 才知道最终答案

执行p(0,5)的时候 知道要调用p(0,2)

p(0,5)的结果没有出来，p(0,5)就进栈了

调p(0,2)的时候 知道自己要先调用p(0,1)

p(0,2)就进栈了

调用p(0,1) 知道先调用p(0,0)所以p(0,1)就进栈了

p(0,0)和p(1,1)计算完之后 p(0,1)就得到结果了

此时p(0,0)和p(1,1)就出栈了

依此类推

悬而未决的东西就会进到栈中

算完的东西就会从栈里弹出

所以就可以认为整个递归过程就是一个多叉树

利用栈玩了一个遍历

每个节点都通过自己的子节点给自己汇总信息之后

才能够继续往上返回

那栈空间就是一个数的高度

只能在一个高度上压栈

这就是递归的过程

本文内容由快快网络小茜创作整理编辑！