两种解方程的方法(方程有两种解法分别是什么)

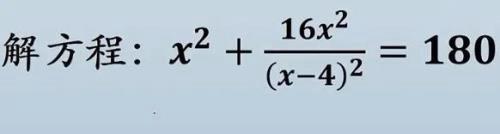
导语：两种解方程方法，为什么结果不-样，糊涂了

分析：x≠4

解法①

令x=a ，4x/（x-4）=b

a+b=x+4x/（x-4）=x^2/（x-4）

ab=4x^2/（x-4）

∴ab=4（a+b）…①

而a^2+b^2=180…②

由②式得：（a+b）^2-2ab=180…③

将①代入③得：（a+b）^2-8（a+b）-180=0

∴[（a+b）+10][（a+b）-18]=0

∴a+b=-10或a+b=18

当a+b=-10时，ab=-40，由韦达定理，a、b为方程m^2+10m-40=0的两根

∴m=-5±√65

∴a=-5+√65或a=-5-√65

∴x1=-5+√65，x2=-5-√65

当a+b=18时，ab=72，由韦达定律，a、b可看作方程m^2-18m+72=0的两根

∴（m-12）（m-6）=0

∴a=12或a=6

∴x3=12，x4=6

∴原方程的解为：x1=-5+√65，x2=-5-√65

x3=12，x4=6

解法②：配平方

原方程可变为：[x^2+2.x.4x/（x-4）+16/（x-4）^2]-8x^2/（x-4）=180

[x+4x/（x-4）]^2-8x^2/（x-4）=180

[x^2/（x-4）]^2-8[x^2/（x-4）-180=0

令x^2/（x-4）=a

则a^2-8a-180=0

（a-18）（a+10）=0

∴a=18或a=-10

当a=18时，x^2/（x-4）=18，即x^2-18x+72=0，（x-12）（x-6）

∴x1=12，x2=6

当a=10时，x^2/（x-4）=10，即x^2-10x+40=0，△<0，无实根

∴原方程的解为：x1=12，x2=6

本文内容由快快网络小畅创作整理编辑！