通过分解加速度求解受力的方法(分解加速度例题)

导语：通过分解加速度求解受力

分解加速度：这种方法一般是在以某个力的方向为x轴正方向时，其他的力都落在或大多数力落在两个坐标轴上而不需再分解力的情况下应用.最常见的情况是与斜面模型结合，物体所受的作用力是相互垂直的，而加速度的方向与任一方向的力不同向.此时，首先分析物体受力，然后建立直角坐标系，将加速度a分解为ax和ay，根据牛顿第二定律得Fx＝max，Fy＝may，最后求解.

【关键点拨】加速度的存在代表合外力的存在，所以将加速度沿所需求的力的方向分解，继而在分力方向上利用牛顿第二定律求解力，此时会是更简便的解决问题的方法.

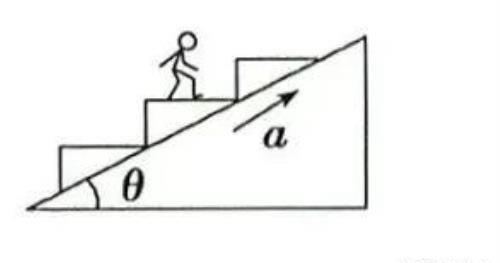
例题1：如图所示，某商场内扶梯与水平面夹角为θ＝30°，质量为60kg的人站在扶梯的水平台阶上，当扶梯以2m/s²的加速度斜向上运动时，求人对扶梯的压力和人所受到的摩擦力各是多少.

例题2：如图所示，细线的一端系一质量为的小球，另一端固定在倾角为θ的光滑

斜面体顶端，细线与斜面平行。在斜面体以加速度a水平向右做匀加速直线运动的过程中，小球始终静止在斜面上，小球受到细线的拉力T和斜面的支持力为FN分别为（重力加速度为g）（）

A:T＝m（gsinθ＋acosθ），FN＝m（gcosθ-asinθ）

B:T＝m（gcosθ＋asinθ），FN ＝m（gsinθ-a cosθ）

C:T＝m（acosθ-gsinθ），FN ＝m（gcosθ＋asinθ）

D:T＝m（asinθ-g cosθ），F m（gsinθ +acosθ）

【练习】

本文内容由快快网络小悦创作整理编辑！