万有引力在高考中重要吗(高考物理万有引力经典题型)
导语:记住以下八点,搞定高考万有引力
天体运动考点总结
一、开普勒定律 万有引力定律的理解与应用
1.开普勒行星运动定律
(1)行星绕太阳的运动通常按圆轨道处理.
(2)开普勒行星运动定律也适用于其他天体,例如月球、卫星绕地球的运动.
(3)开普勒第三定律=k中,k值只与中心天体的质量有关,不同的中心天体k值不同.
2.万有引力定律
公式F=G适用于质点、均匀介质球体或球壳之间万有引力的计算.当两物体为匀质球体或球壳时,可以认为匀质球体或球壳的质量集中于球心,r为两球心的距离,引力的方向沿两球心的连线.
二、万有引力与重力的关系
1.地球表面的重力与万有引力
地面上的物体所受地球的吸引力产生两个效果,其中一个分力提供了物体绕地轴做圆周运动的向心力,另一个分力等于重力.
(1)在两极,向心力等于零,重力等于万有引力;
(2)除两极外,物体的重力都比万有引力小;
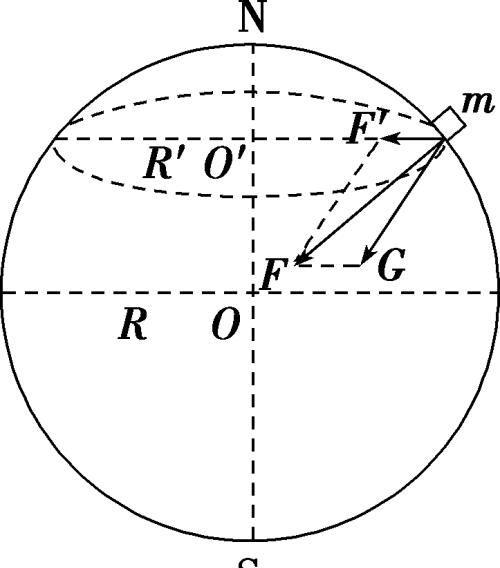
(3)在赤道处,物体的万有引力分解为两个分力F向和mg刚好在一条直线上,则有F=F向+mg,所以mg=F-F向=-mRω.
2.星体表面上的重力加速度
(1)在地球表面附近的重力加速度g(不考虑地球自转);mg=G,得g=.
(2)在地球上空距离地心r=R+h处的重力加速度为g′,mg′=,得g′=
所以=.
三、中心天体质量和密度的估算
中心天体质量和密度常用的估算方法
应用公式时注意区分"两个半径"和"两个周期"
(1)天体半径和卫星的轨道半径,通常把天体看成一个球体,天体的半径指的是球体的半径.卫星的轨道半径指的是卫星围绕天体做圆周运动的圆的半径.卫星的轨道半径大于等于天体的半径.
(2)自转周期和公转周期,自转周期是指天体绕自身某轴线运动一周所用的时间,公转周期是指卫星绕中心天体做圆周运动一周所用的时间.自转周期与公转周期一般不相等.
四、卫星运行参量的比较与计算
1.卫星的轨道
(1)赤道轨道:卫星的轨道在赤道平面内,同步卫星就是其中的一种.
(2)极地轨道:卫星的轨道过南北两极,即在垂直于赤道的平面内,如极地气象卫星.
(3)其他轨道:除以上两种轨道外的卫星轨道,且轨道平面一定通过地球的球心.
2.地球同步卫星的特点:六个"一定"
3.卫星的各物理量随轨道半径变化的规律
4.解决天体圆周运动问题的两条思路
(1)在中心天体表面或附近而又不涉及中心天体自转运动时,万有引力等于重力,即G=mg,整理得GM=gR2,称为黄金代换.(g表示天体表面的重力加速度)
(2)天体运动的向心力来源于天体之间的万有引力,即
G=m=mrω2=m=man.
五、宇宙速度的理解与计算
1.第一宇宙速度的推导
方法一:由G=m得v1==7.9×103 m/s.
方法二:由mg=m得v1==7.9×103 m/s.
第一宇宙速度是发射地球人造卫星的最小速度,也是地球人造卫星的最大环绕速度,此时它的运行周期最短,Tmin=2π≈85 min.
2.宇宙速度与运动轨迹的关系
(1)v发=7.9 km/s时,卫星绕地球表面附近做匀速圆周运动.
(2)7.9 km/s<v发<11.2 km/s,卫星绕地球运动的轨迹为椭圆.
(3)11.2 km/s≤v发<16.7 km/s,卫星绕太阳做椭圆运动.
(4)v发≥16.7 km/s,卫星将挣脱太阳引力的束缚,飞到太阳系以外的空间.
六、近地卫星、赤道上的物体及同步卫星的运行问题
三种匀速圆周运动的参量比较
七、双星及多星模型
1.模型特征
(1)多星系统的条件
①各星彼此相距较近.
②各星绕同一圆心做匀速圆周运动.
(2)多星系统的结构
2.思维引导
八、卫星的变轨问题
人造地球卫星的发射过程要经过多次变轨,如图所示,我们从以下几个方面讨论.
1.变轨原理及过程
(1)为了节省能量,在赤道上顺着地球自转方向发射卫星到圆轨道Ⅰ上.
(2)在A点点火加速,由于速度变大,万有引力不足以提供在轨道Ⅰ上做圆周运动的向心力,卫星做离心运动进入椭圆轨道Ⅱ.
(3)在B点(远地点)再次点火加速进入圆形轨道Ⅲ.
2.物理量的定性分析
(1)速度:设卫星在圆轨道Ⅰ和Ⅲ上运行时的速率分别为v1、v3,在轨道Ⅱ上过A点和B点时速率分别为vA、vB.因在A点加速,则vA>v1,因在B点加速,则v3>vB,又因v1>v3,故有vA>v1>v3>vB.
(2)加速度:因为在A点,卫星只受到万有引力作用,故不论从轨道Ⅰ还是轨道Ⅱ上经过A点,卫星的加速度都相同.同理,从轨道Ⅱ和轨道Ⅲ上经过B点时加速度也相同.
(3)周期:设卫星在Ⅰ、Ⅱ、Ⅲ轨道上运行周期分别为T1、T2、T3,轨道半径分别为r1、r2(半长轴)、r3,由开普勒第三定律=k可知T1<T2<T3.
(4)机械能:在一个确定的圆(椭圆)轨道上机械能守恒.若卫星在Ⅰ、Ⅱ、Ⅲ轨道的机械能分别为E1、E2、E3,则E1<E2<E3.
本文内容由快快网络小洁整理编辑!