问题 设D为一平面区域，L为不穿过D内部的共面直线，求D绕L旋转一周所成旋转体的体积。

结论 由连续曲线y=f(x)，其中f(x)≥0，以及直线x=a，x=b及x轴所围成的曲边梯形D绕不穿过曲边梯形内部的共面直线L：Ax+By+C=0旋转一周所成的旋转体的体积为：

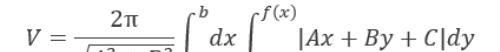
证明 曲边梯形D上任取一点P(x,y)，则x,y的变化范围为0≤y≤f(x)；a≤x≤b.点P(x,y)到L的距离

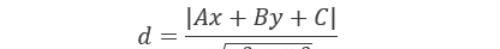
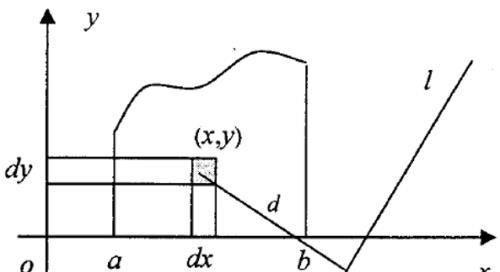
在点P(x,y)处分别给出x,y的微分dx,dy，得曲边梯形上的面积微元dσ，且知dσ=dxdy。面积为dσ的面积微元绕L旋转所形成的立体体积微元

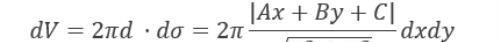
所以有

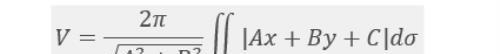
几种特殊情形

(1) D: g(x)<y<f(x), a<x<b时

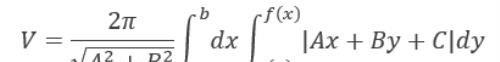
(2) D: u(y)<x<v(y), c<y<d时

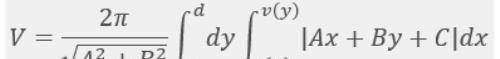
(3) D: r1(q)<r<r2(q), a<q<b时

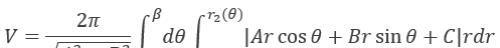
(4) D: 0<y<f(x), a<x<b, 且L为y轴时

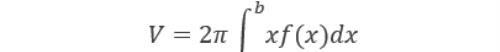
(5) D: 0<r<r(q), a<q<b, 且L为x轴或极轴时

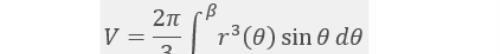
(6) D: 0<y<f(x), a<x<b, 且L为x轴时

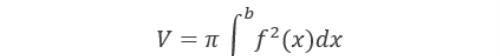
例子

1. 求椭圆x2+2y2=1绕直线x+y=2旋转一周所成旋转体的体积。

解 平面区域D可表示为：

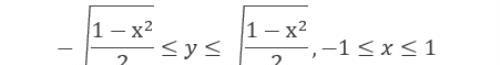
区域D与直线x+y=2的位置关系如下图：

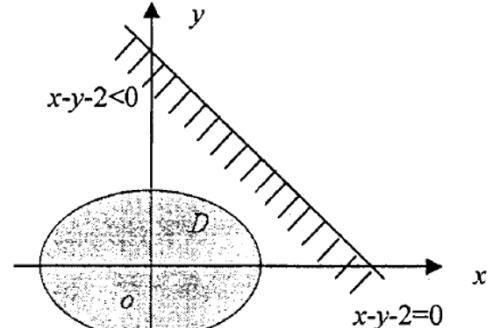
对区域D内任意点都有：x + y –2<0，所以

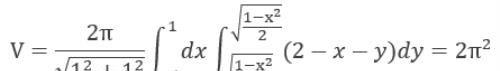
2. 求心形线r=4(1+cosθ)及射线θ=0及θ=π/2所围成的图形绕极轴旋转一周所成旋转体的体积.

解 区域D为：

0<r<4(1+cos θ), 0<θ<π/2

对D内任意点都有y>0，所以有

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请与我联系，一经查实立刻删除内容。本文内容由快快网络小嫣创作整理编辑！