递归函数的时间复杂度是多少(递归算法的时间复杂度怎么计算)

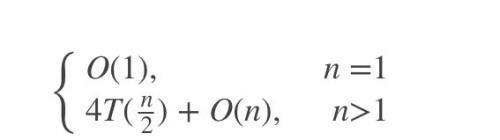
导语：一举弄懂递归函数的时间复杂度

对于计算机科学来说，算法至关重要。通俗地讲，算法是指解决问题的一种方法或者一个过程。严格来讲，算法是由若干条指令组成的有序序列，且满足以下4条性质：

1.输入

2.输出

3.确定性

4.有限性

算法复杂度的高低体现在运行该算法时所需要的计算机资源的多少上，所需资源越多，算法的复杂度越高，也就称这个算法较差。因此，算法的复杂度分为时间复杂度和空间复杂度。

由于空间复杂度是具体算法具体分析，因此这里我们简单谈一谈时间复杂度。

普通函数的时间复杂度大致分为4个步骤：确定循环条件->确定循环变量的变化规律->假设执行了i次->计算i并带回原方程。

遵循了上述四个步骤就能求解大部分的算法时间复杂度了。

对于递归函数，我们举一个简单的例子来说明。

这是一个求解大整数乘法的递归表达式，对于它的时间复杂度，其计算过程如下：

T(n)=4T(n/2)+O(n)

=4[4T(n/4)+O(n/2)]+O(n)=4^2T(n/4)+3O(n)

=4^2[4T(n/8)+O(n/4)]+3O(n)=4^3T(n/8)+7O(n)

......

=4^xT(n/2^x)+(2^x-1)O(n) //假设执行了x次

令n=2^x 带入上面方程 T(n)=n^2+(n-1)n

因此时间复杂度为O(n^2)

再看下面这个

这是对大整数乘法的另一种优化算法，具体思想我就不再这里赘述了

对于这个表达式，我们还是按照上面的方法一步一步的来

T(n)=3T(n/2)+O(n)

=3[3T(n/4)+O(n/2)]+O(n)=3^2T(n/4)+(3/2 +1)O(n)

=3^2[3T(n/8)+O(n/4)]+(3/2 +1)O(n)=3^3T(n/8)+(3^2/2^2 +3/2 +1)O(n)

……

=3^xT(n/2^x)+(3^x-1/2^x-1 +3^x-2/2^x-2 +......+3^2/2^2 + 3/2 +1)O(n)

易知后面括号里其实是首项为1，公比为3/2的等比数列的前n-1项和

因此上式

=3^xT(n/2^x)+[4(3^x-1 /2^x)-2]O(n)

令n=2^x ，则x=log2(n),带入

=3^log2(n)+{4[(3^log2(n/2))/n]-2}O(n)

=n^log2(3)+4/3 (n^log2(3)) -2n

=5/3 n^log2(3) -2n

u 因此时间复杂度为O(n^log2(3)) =O(n^1.59)

因为O(n^1.59)<O(n^2)

所以后面这种算法是优于前面那一种算法的。

你看，都是解决大整数乘法的问题，通过不同的算法，我们求解问题所花的时间也不同，所以，在计算机的发展中，寻找最优算法是一直在路上的。

本文内容由快快网络小樊创作整理编辑！