线段数量关系探究的思考方法有哪些(线段数量关系探究的思考方法和技巧)

导语：线段数量关系探究的思考方法

考试中，有一类题是探究线段的数量关系。

大致可分为两类：两条线段的数量关系（有时候还要探究位置关系，一般是垂直或者平行）和三条线段的数量关系。

两条线段的数量关系常见的有：①相等；②2倍；③根号2倍；④根号3倍等。

三条线段间的数量关系：①最长的等于其余两条之和（和差是等价的，线段前的系数均为1）；②等式之间线段前的系数不全是1（这类难度大）

一般情况下，题目中给出关系进行证明，相对容易一些。（只是相对）

难题是要自己判断出数量关系，并加以证明。若判断出（可能也是猜测的），证明会相对容易一些，否则方向都找不到，无从证明。

证明线段相等，通常（不是绝对）要利用全等三角形，难点是如何寻找出全等三角形；

证明两条线段间存在倍数关系（不一定是整数倍），比如2倍（对应1/2）要考虑中位线、斜边中线的性质等，当然还有特殊角度（30°，60°）。看见根号2，要想到构造等腰直角三角形（45°）等等。有时用相似形也能快速证明两条非等长线段之间的数量关系。

三条线段间的数量关系终极目标是将三条线段转换到一个图形中：这个图形可以是直线（线段间的数量关系用和差就可表示出来），也可是一个特殊的三角形（比如直角三角形，线段间的数量关系可用）勾股定理表示。

转移的方法往往涉及到平移、对称、旋转、相似等变换，需要平时积累。通过积累掌握一些经典模型，这点很重要。（可见平时练习的重要性）

判断线段间数量关系有一个重要的方法：特殊值。符合题意的情况下，寻找一个特定的点或者角度进行判断，然后进行一般证明。

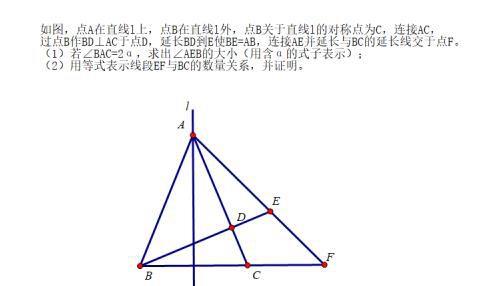
下面这道题是判断两条线段间的数量关系：

第1问是典型的倒角类题型，方法很多，要注意利用等腰三角形顶角和底角之间的数量关系。

可得∠AEB=45°+α（可以借此机会把其他角度也算算，发现∠EFC=45°，这个发现很重要！）

第2问，可以用有刻度的直尺量一下EF和BC（一般考试提供的图形都是比较准确的），发现它们是不相等的。

根据第1问发现的∠EFC=45°，猜测BC=√(2)EF

（采用特值法判断：由于题目没有限定点B的位置，可以考虑到当∠BAC=90°时，发现点E和A重合，点C和F重合，判断出BC=√(2)EF；当∠BAC=0°时，EF和BC均为0,无法判断)

注意上面这种特值法的经验积累，对解题会有帮助。

判断出BC=√(2)EF，难度降低一半，证明方法很多，这里提供一种。

这种构造方法要充分利用特殊角度

通过全等三角形进行线段的转换

详细解题过程略去。

下面再看几道三条线段之间数量关系的题：线段间数量关系的系数为1

基于等边三角形（和四点共圆）

线段间数量关系的系数不为1

基于等腰直角三角形（和四点共圆）

上述两类图形可作为三条线段间数量关系探究的经典练习题。

小结：三条线段间的数量关系判断一定要设法转到同一条直线或者同一个图形（比如直角三角形）。

本文内容由小蔼整理编辑！