初中动点轨迹问题集锦(初中动点运动轨迹判断)

导语：初中阶段动点轨迹分析思路

动点的运动轨迹（路径）是初中几何的常考点和难点。

在初中阶段、常见的动点轨迹主要有两种形式：直线和圆。

如果题目中直接已知动点在直线或者圆上，不是我们要讨论的问题。

题目中往往是给定一些特定的描述，要求我们能判断出动点的轨迹。

先看看轨迹为圆（或者圆的一部分）的一些典型形式：

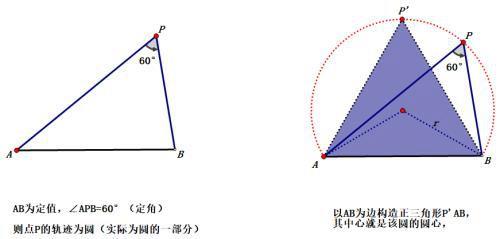
定线对定角模型：

轨迹为圆的一部分

还有这种：

轨迹为半圆

还有一种根据圆的定义（到定点距离为定长）：

根据圆的定义，确定动点的轨迹

轨迹为直线型的比较经典的有：中垂线的性质，角平分线的性质，平行线间距离相等。

还有在平面直角坐标系中，点P（m+1,2m-3）,翻译成几何语言就是点P在直线y=2x-4上运动

还有一种通过旋转，形成的直线型：

点C的轨迹实际上一条射线

题目要求OC的最小值，通常要判断点C的轨迹。如果能够判断出来，则问题比较好解决。

关键是如何判断点的轨迹及具体位置。

网上有很多这方面的资料，就是所谓的瓜豆模型，可以查询总结。

其中涉及到最主要的变换是旋转变换：通过旋转形成全等三角形或者相似三角形。

（全等三角形就是相似比为1:1的相似三角形，所以这类问题的本质都是构造相似）

构造的主要思路（作辅助线）大部分都是通过SAS型进行。

可以理解为：图中有什么样的三角形（以等腰直角和正三角形最为常见），就需要构造一个确定的类似三角形。

（题目中出现了等腰直角三角形就要想法构造一个确定的等腰直角三角形；出现了正三角形就要构造一个确定的正三角形。之所以强调“确定的&39;也是正三角形

注意到线段AO&39;⊥AO’，因此CO‘的位置也是确定（与x轴的夹角为30°）

问题转化为求点到直线的最小值，这就很好解决了

小结：通过旋转确定动点轨迹，需要事先构造出一个确定图形，然后再证明这样的图形能够满足解题的需要。

再看一例：

根据上述思路，需要找到一个确定的等腰直角三角形。

做法如下：

本文内容由快快网络小故整理编辑！