完成正方形abcd的投影(正方形abcd求阴影部分面积)

P是BC边上的动点，以点P为圆心，PM长为半径作圆P,当圆P与正方形ABCD的边相切时，斜边上的高是两条直角边在斜边射影的比例中项，有∠EMC＝90°，因当MB⊥BC，MB²＝EB·BC：则圆直径EC＝2＋8＝10，圆半径EP＝10/2＝5，设BP=x，解得x=3，当圆P与直线AD相切时，设切点为K，所以四边形P-C-D-K是矩形，所以PM=CD=8，由于M为AB中点：

导语：“射影定理”专题，正方形ABCD与圆P相切，求BP的长是多少

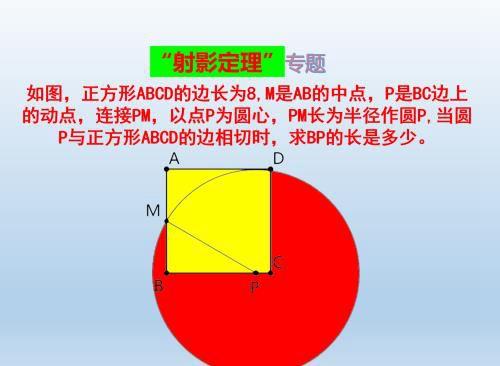
题目：如图，正方形ABCD的边长为8,M是AB的中点，P是BC边上的动点，连接PM，以点P为圆心，PM长为半径作圆P,当圆P与正方形ABCD的边相切时，求BP的长是多少。

射影定理：射影定理，又称“欧几里德定理”：在直角三角形中，斜边上的高是两条直角边在斜边射影的比例中项，每一条直角边又是这条直角边在斜边上的射影和斜边的比例中项。

解法1：延长CB交⊙P于E，连接ME、MC，有∠EMC＝90°，因当MB⊥BC，依射影定理有：MB²＝EB·BC，即16＝EB·8，EB＝2，则圆直径EC＝2＋8＝10，圆半径EP＝10/2＝5，则BP＝EP一EB＝5一2＝3。

解法2：当圆P与CD相切时，设BP=x，则PM=PC=8-x，有x²+4²=（8-x）²，解得x=3 ，当圆P与直线AD相切时，设切点为K，连接PK，则PM=PK。因为K为切点， 所以PK垂直AD，所以四边形P-C-D-K是矩形，所以PK=CD，所以PM=CD=8，所以BP=✓(PM²-BM²)=✓(8²-4²)=4✓3 ,综上所述，BP的长是3或4✓3。

解法3：由于M为AB中点，P在BC上 ，⊙P与正方形ABCD相切有两种情形，①⊙P与AD相切，PM＝AB ,有BP²＋4²＝8²，得BP＝4√3 ，②⊙P与CD相切，PM＝PC，有BP²＋4²＝(8一PB)²，得PB＝3 ，综上述：PB长为3或4√3.

免责声明:本文由原创用户编辑投稿，若来源犯您的合法权益,请与我们取得联系，我们更正修改。2023年04月08日由小涵整理编辑！