任意角的三角函数有什么用(任意角的三角函数的概念)

导语：任意角的三角函数，借助于单位圆更容易理解

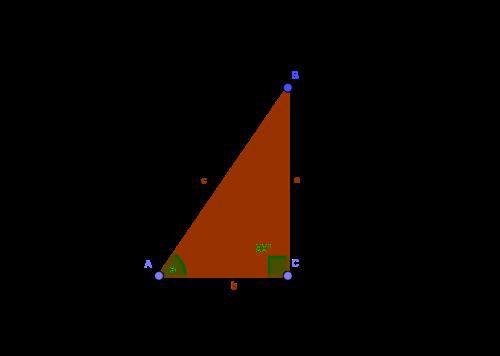
1.直角三角形中的锐角三角函数

初中数学中第一次接触三角函数，是为了在直角三角形中表示边长之间的关系。

在图中的直角三角形中

角度α的范围为0°~90°，即弧度0~π/2，可以将上述三角函数看作自变量取值范围为(0, π/2)的函数。

2.任意角的三角函数

锐角三角函数的局限性太明显了，与上篇文章《角度扩展之任意角与弧度角》中角的范围扩展类似，三角函数的自变量取值范围也可以相对应地扩充到整个实数集。

现在我们来重新定义三角函数，将角的范围扩充。以原点A为圆心作半径为r的圆，圆上任意一点B的坐标为(x, y)，半径AB与x轴形成夹角α（实数集上的任意角），则定义

上述定义中，正弦函数和余弦函数对任意实数角都存在函数值，正切函数要求x不能为0，其自变量的取值范围应为

3.单位圆中的三角函数

上述定义中涉及到圆的半径r，由于r可以取任意正实数值，为了更加简化三角函数的定义，我们令r=1。

即在圆心在原点的单位圆中，任意角的三角函数定义简化为

正切函数的角仍然不能为π/2的奇数倍。

这样一来，我们就把三角函数的定义域扩充到实数域之内。根据任意角的定义，单位圆上任意一点都对应无数多个角度，它们之间的差值为2π的整数倍。换个角度理解就是，相差为2π的角对应的正弦值、余弦值、正切值都相同。正弦函数、余弦函数在实数范围内是周期为2π的周期函数，而正切函数实际上为周期为π的周期函数。

本文内容由小樊整理编辑！