大话数据结构平衡二叉树纠错(平衡二叉树怎么构建)

导语：大话数据结构之平衡二叉树

我又开始发表文章了，很抱歉停了很长一段时间。确实这段时间是比较忙，朋友找我帮忙开发游戏，主要是U3D，使用C，更没接触过游戏开发。这次也算是职业上的一次转变，付出很多，也收获很多。后面有机会，可以发一点相关的文章，来和大家一起成长。

今天还是继续写一点基础的东西，继上次的二叉树，这次还是讲和二叉树相关的知识点——（AVL）平衡二叉树。顾名思义，平衡二叉树意思就是左子树和右子树差不多的一种二叉树。

下面给出定义：平衡二叉树，是一种特例的二叉树，其所有节点的左右子树深度都不超过1。

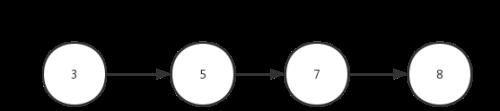
普通二叉树在极端情况下，有可能变成单链表，如下图：

单链表

如果是单链表，对于二叉树来说，查找二叉树变成线性的，那就完全没有意义了。所以，今天和大家一起来学习平衡二叉树。首先，我们定义下平衡因子，即左子树的高度减去右子树的高度。如图所示：

正如，平衡二叉树的定义，我们需要保证二叉树所有节点的平衡因子只能是-1、0和1（上图右边的二叉树是不平衡的）。在数据结构中，我们通常的操作一般都有插入、删除和查找。这里我们首先讲插入，一棵树的创建就是不断插入的一个过程，当我们往一个平衡二叉树插入一个新的子节点，可能造成平衡二叉树的失衡，即存在有节点的平衡因子为2或者-2的状态，因此我们需要调节二叉树，使之保持平衡。

通常会出现四种情况，因此需要四种操作来平衡二叉树。

右旋（Right Rotation）

当有节点的平衡因子为2时，说明左边子树深度大于右边，因此需要右旋。

左旋（Left Rotation）

当有节点的平衡因子为-2时，说明右边的子树的深度大于左边，因此需要左旋。

右左旋

在这种情况下，单纯的左旋不能使二叉树平衡，这里使用右左旋，先让子树（4和6）右旋，然后整体再左旋。

左右旋

同上，先让子树（2和4）左旋，再整体右旋。

上面介绍了四种操作方法，但具体什么情况使用什么操作，这里再和大家详细介绍一下。当节点的平衡因子大于2时，说明是左子树深度偏大，此时需要右旋或者左右旋。右旋操作不仅会使父节点降低平衡因子，也会降低左节点的平衡因子。所以当父节点平衡因子为2，而左子节点的平衡因子小于0时，如果使用右旋，得到的二叉树还是一个不平衡的二叉树，所以需要先对左子树进行左旋，然后整体右旋，即左右旋操作。

这里，给出一个平衡二叉树的伪代码，大家仔细体会一下：

下面给出代码（C语言）：

首先定义结构体

扩展方法

核心代码

插入方法

Main方法

输出截图

本文内容由快快网络小岑创作整理编辑！