对于几何问题，欧几里得有非常重要和有力的解题工具，那就是相似三角形和全等三角形。全等三角形是特殊的相似三角形，就是说两个相似三角形的相似比如果是1：1，那么，它们是全等三角形。

今天的主题是全等三角形。我们首先看一道题（欧几里得的风车），它的证明很难，也是几百年前的欧洲大学生要学习的内容，也让当时的差生抓狂。

我们学习全等三角形的几个知识点以后，进入中学数学讲座：全等三角形的自述。学习后，我们来攻克欧几里得的风车这道难题，见识全等三角形的威力。

《天才引导的历程》截图

题目：欧几里得的风车

如图，利用欧几里得作的5条辅助线，证明对于直角三角形，勾股定理成立。

全等三角形的相关知识点

图形的全等（congruence of figures）

图形间的一种等价关系，给定平面上或空间中的两个几何图形，如果经过合同变换（即正交变换），一个图形能与另一个图形重合，即一个图形能变成另一个图形，则说这两个图形全等或合同（也可说成图形相等）,并把这两个图形称为全等（图）形或合同（图）形.例如，平面上有线段、角、三角形、圆等的全等，空间中有多面角、多面体、球等的全等.两个图形F₁ 和F₂全等，记为F₁≌F₂或F₁≡F₂，图形的全等是等价关系，即具有：

1．反身性：对于任何图形F，有 F≌F.

2．对称性：对于图形F₁ 和F₂，若 F₁≌F₂，则F₂≌F₁.

3．传递性：对于图形F₁, F₂, F₃，若 F₁≌F₂ , F₂≌ F₃，则F₁≌F₃.

两个全等形重合时其重合的几何元素称为对应元素，如对应点、对应边、对应角等.两个全等形，若经过的变换只包括平移和旋转，即经过刚体运动（即第一种正交变换）而重合，则称为正向全等形或同向全等形；若经过的变换必须包括一个（且只有一个）反射（即不是刚体运动）才能重合，则称为逆向全等形或反向全等形.特别是只经过一次反射而重合的反向全等形，在空间中是经过镜面反射，因此在立体几何中把这种反向全等形称为镜像全等形或镜照全等形.

三角形的全等（ congruence of triangles ）三角形间的等价关系.两个三角形的全等是指图形的全等，即它们经过合同变换能完全重合.这两个三角形也称全等三角形.△ABC 和 △A&39;C&39;B&39;A ，读作△ABC 全等于△A&39;C“ ASA “ SSS ”。此外，对于特殊的三角形还可以特别对待。如对于两个直角三角形，若一条直角边和斜边对应相等，就可以直接判定他们全等，简称为“ HL ”。

别看我们的判定方法多，其实还是有一定规律的。通过三角形位置变换：平移、翻折、旋转，能很方便就找到两个三角形对应相等的元素。

平移：将其中一个三角形沿某一直线平移一定距离，与另一个三角形相互重合，从而发现对应相等的边和角。如图2、图3, △DEF 是由△ABC 向右平移而得，从而有 DE = AB 、 EF = BC 、 DF = AC 。

图2 图3

翻折：将其中一个三角形沿某一条直线翻折，与另一个三角形相互重合，从而发现对应相等的边和角。如图4,△DBC 是由△ABC 沿 BC 翻折而得，从而有 BD = AB 、 DC = AC ；同样，图5一图8中的△DFE 都是由△ ABC 沿某条直线翻折得到的。

图4 图5 图6 图7 图8

旋转：将其中一个三角形绕某一点，向某一方向旋转一定角度后，与另一个三角形相互重合，从而发现对应相等的边和角。如图9、图10, △AEF是由△ABC绕点A逆时针旋转一定角度而得。同学们可以试着找出对应边和对应角。

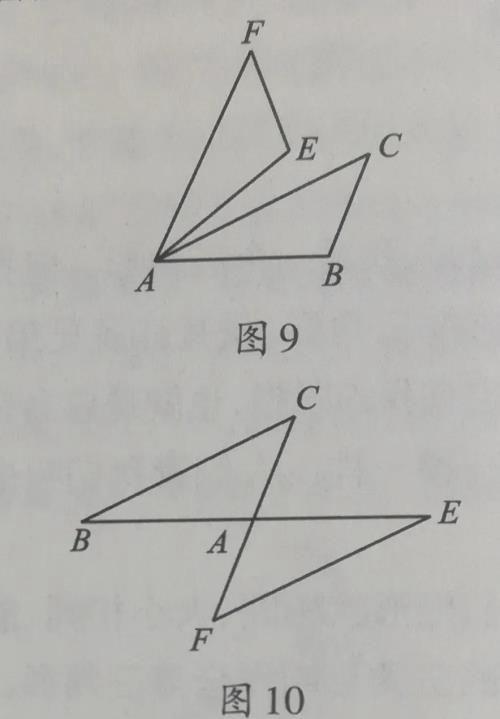
图9 图10

判定我们全等的路线图如下：

1.已知两边

1.1找夹角（ SAS )

1.2找直角（ HL )

1.3找第三边（ SSS )

2.已知一边一角

2.1边为角的对边，找任意角（ AAS )

2.2边为角的邻边

2.2.1找已知角的另一边（ SAS )

2.2.2找已知边的对角（ AAS )

2.2.3找夹已知边的另一角（ ASA )

3.已知两角

3.1找两角的夹边（ ASA

3.2找任意一边( AAS )

图11

此外，用我们的判定方法和性质，可以证明两个角相等或两条线段相等。如果要证明两个角或两条线段的数量或大小关系，同学们可要想到我们哦！

（作者单位：江苏省泰州市第二中学附属初级中学）

全等三角形的威力

应用全等三角形解题的例子不胜枚举，下面我们来攻克欧几里得的风车这道难题，验证全等三角形的巨大威力。

欧几里得的风车

上图是欧几里得证明勾股定理的名场面。为解决本题，欧几里得作了5条辅助线，为了清晰易懂，下面的解答图只有三条辅助线。省略的部分可用“同理可证”代替。

解答图

注意，因为上图粗线三角形是直角三角形，所以点A、C、G三点共线，点A、B、H也是三点共线。

综观欧几里得的精彩论证，源自全等三角形的证明，之后证明了射影定理，于是勾股定理的证明就水到渠成。

全等三角形

注意观察，三角形BCF绕顶点B顺时针旋转90°后，与三角形BDA重合，易证它们是全等三角形。

因为等底等高的两个三角形面积相等，所以，同底三角形的第三个顶点在与底边平行的直线上滑动，得到的所有三角形都面积相等。

根据这个道理，又因为矩形的对边是平行的，所以，△FBG和△FBC面积相等。同理可证，△BDA和△BDM面积相等。

因为△BDM面积为以BL为对角线的矩形面积的½，

因为△FBG面积为正方形的½，所以矩形BL的面积等于正方形FA。

于是证明了射影定理：AB²=BM·BC，因为ML把大正方形分为两个矩形，根据射影定理，这两个矩形面积分别等于对应的正方形面积，从而证明了勾股定理。

欧几里得的这个经典证明非常精彩，也充分发挥了全等三角形的威力。希望同学们认真学习并掌握全等三角形的知识，并能够熟练应用。

科学尚未普及，媒体还需努力。感谢阅读，再见。

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请与我联系，一经查实立刻删除内容。本文内容由快快网络小春创作整理编辑！