一道三角形的证明题几种解法怎么做(三角形证明题100道及答案)

一道三角形的证明题：

在 ΔABC; AB=AC, ∠BAC=120∘, 且 BC=√5 D 是ΔABC内部的一个点，并且有BD=1和CD=√2

求证：∠ADC=60∘.

证法1：这个思路很直接，就是要求出AD的长度，因为如果知道三边，可以求出三角形的任意一个角。而要求出AD，就需要求出图中角贝塔β的余弦值，因为已经知道它的两个边长。而β=30°-α， 所以cosβ=cos(30°-α), 而角α的余弦可用余弦定理求得。因此可以求得角ADC。

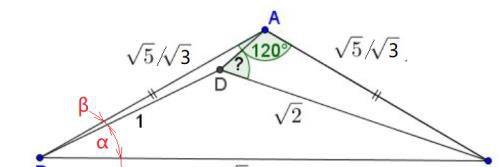
先求cosα, 在三角形BDC中，有：

1+5-2x1xcosα=2, 解得：

Cosα=2/, 那么sinα=1/

所以

cosβ=cos(30°-α)

=cos30°cosα+sin30°sinα

=/2x 2/+1/2x 1/

=(2+1)/2

在三角形ABD中利用余弦定理有：

=5/3+1-2x1x/cosβ, 解得：

AD=(-1)/

最后在三角形ADC中，有

cos∠ADC=(+-)/2AD.CD=1/2,

即证出∠ADC=60°

证法2：

将图形点A反时针旋转120，B点到C, C到C′, 且 D to D′.

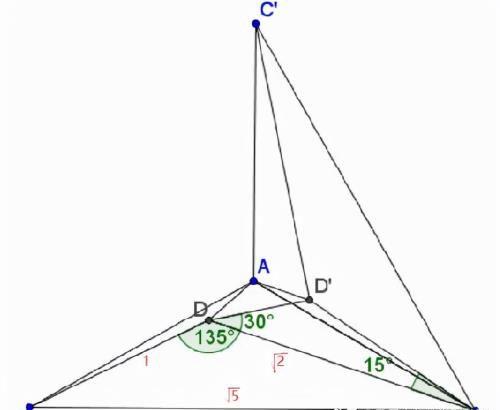
在ΔBCD中根据余弦定理,

5=1−2√2cos∠BDC+2,

求出cos∠BDC=−√2/2，所以∠BDC=135∘.

这样我们可以推出∠CBD+∠BCD=180°-135°=45°,

∠C′CD′=∠CBD,

∠BCC′=30°+30°=60°,

由此推出∠DCD′=60°-（180°-135°）=15°.

我们知道利用半角公式:

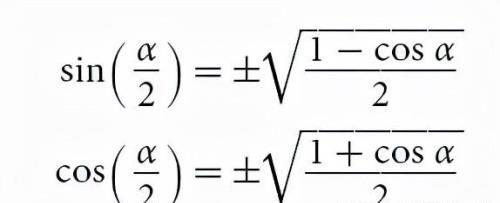
可以求出sin15°与cos15°

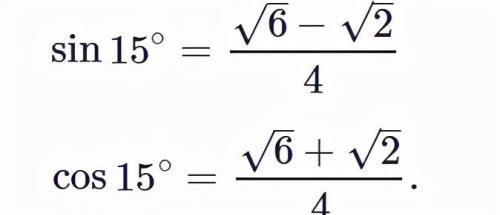
因为CD′=BD=1, 在ΔDCD利用余弦定理可求出DD′:

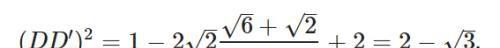
随后在ΔDCD′利用正弦定理,

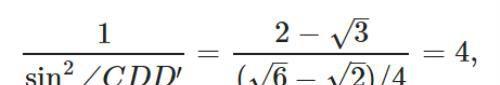
因此求出∠CDD′=30°.

注意到三角形ADD’的顶点为120度，这是由于旋转的对称性决定的

即, ∠DAD′=120° 且 AD=AD′，

那么∠ADD′=30°

所以∠ADC=60°.

证法3：把各点看成复数，选择：

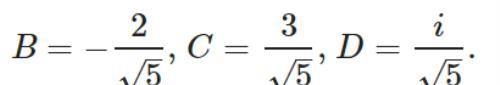
那么在这种设定下A的复数：

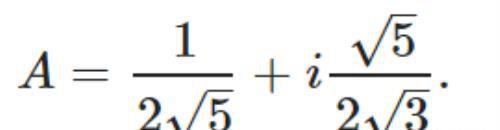
令ϕ=∠ADC，做两个复数的除法：

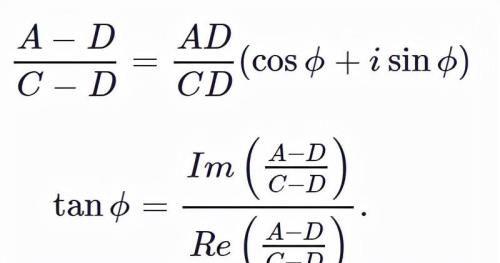
这样得到：

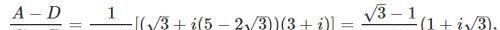
由此推出：

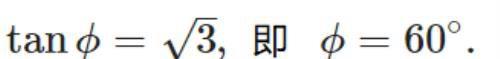
免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请与我联系，一经查实立刻删除内容。本文内容由快快网络小嫣创作整理编辑！