坐标系中的平行四边形的知识(坐标系中平行四边形面积公式)

导语：坐标系中平行四边形，八年级数学

八年级数学坐标系中平行四边形，初二数学

中考题里经常会把各种几何图形放在坐标系中，而平行四边形是最常见的图形之一。为了在坐标系中研究平行四边形，我们需要一些基础知识。平面直角坐标系中的

中点公式平移线段两点间距离公式

下面研究一下平行四边形四个顶点坐标间的关系。

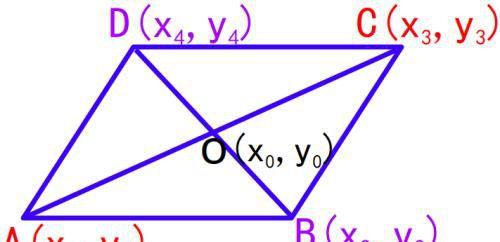
平面直角坐标系中，平行四边形两组相对顶点的横坐标之和相等，纵坐标之和也相等。

简证：如下图平行四边形ABCD，对角线AC与BD交于点O。

(一)根据平行四边形性质，对角线互相平分，所以对角线交点O既是AC中点，又是BD中点。

根据中点公式可得：

(二)也可以根据平行四边形性质：对边平行且相等，采用平移线段的方法来理解，平行四边形ABCD可以理解为AD平移到BC而得。根据平移性质可知

即坐标差相等。移项整理之后结果是一样的。

常见题目，平行四边形存在性：已知3个顶点坐标，求第4个顶点坐标。注意下面两个例题的区别，注意题目中的细节。

例题1：在直角坐标系中，已知平行四边形ABCD，A(1，1)，B(3，1)，C(2，2)，求D点坐标。

注意题目中已经描述平行四边形ABCD(字母有顺序)，即一般默认从某一顶点开始，逆时针顺序描述，所以此时点D只有一种情况。

例题2：在直角坐标系中，点A(1，1)，B(3，1)，C(2，2)，若存在点D使以这四点为顶点的四边形是平行四边形，求D点坐标。

注意此题中没有说明平行四边形的字母有顺序，所以点D有三种情况，需要分类讨论！通常按照对角线来分类：

AB为对角线时，点D(2，0)

AC为对角线时，点D(0，2)

BC为对角线时，点D(4，2)

常见动点题型

三定一动

已知三个顶点坐标，求第四个顶点的坐标，使它们构成平行四边形

第四个顶点(m，n)有两个未知数，根据上面两组相对顶点的关系可以得到两个方程，可解。

两定两动

已知两个顶点坐标，求另外两个顶点的坐标，使它们构成平行四边形

只知道两个定点，这个平行四边形是无法确定的，所以题目中会给出一些其它条件，例如两个动点一个在x轴上，一个在y轴上，这样两个动点可以表示成(m，0)，(0，n)，根据上面两组相对顶点的关系可以得到两个方程，可解。注意结果不能有三(四)点共线。

甚至还有一定三动，四动。多个动点虽然看起来很难，但是都会有其它的限制条件，不要被动点个数吓到。

♡♡♡感谢大家的支持♡♡♡

免责声明:本文由原创用户编辑投稿，若来源犯您的合法权益,请与我们取得联系，我们更正修改。2023年04月08日由小萱整理编辑！