圆微分(圆的微分方程怎么求)

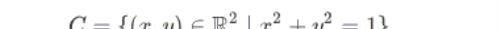
导语：y1.圆上的微分

（文章序列号：y1）

话题：

小石头/编

虽然积分的源头可以追溯到古希腊时期阿基米德对圆周率π的计算，但是我们今天要讨论的主题：圆上的微分，却是近代黎曼之后才逐步建立起来的。

要研究圆上的微分，首先要在圆上搭建一个微分体系，学过《解析几何》的朋友都知道，

正是二维平面（记为，ℝ²）中单位圆上的点组成的集合，于是接下来，闲话不说，直接在C上开搭，走起！

为了方便，将C处于X轴上方的部分叫做北半圆（记为，Cɴ) ，显然Cɴ 是ℝ²的上半平面

与C的交集，即，

令，

是一维直线（记为，ℝ）中的单位开区间。可构建从I到Cɴ的映射（记为，ψɴ:I→Cɴ），

该映射使得I和Cɴ中的点恰恰好一一对应，故它是一一到上的双射。

图1：北半圆的参数化

映射ψɴ和函数的区别是其值是ℝ²中向量而非ℝ中的实数，实际上，ψɴ是由两个函数组成的向量，即，

所以我们一般称ψɴ为向量函数。

将《高等数学》（简称《高数》）中的函数连续性，移植到向量函数上：

◆ 如果一个向量函数的所有组成函数都是连续的，则称这个向量函数是连续的。

根据这个定义，由于函数 x(u)=u 和 y(u)=√(1-u²) 在定义域I内都是连续的，故ψɴ是连续映射。另一方面，ψɴ的逆映射（记为，ψɴ⁻¹：Cɴ→I），

是一个二元函数，《高数》的多元函数连续性知识，告诉我们它也是连续的。

注：多元函数的参数其实就是向量，故也称多元函数为向量函数。

这样我们就在I和Cɴ之间搭建了一个双射ψɴ，并且ψɴ和ψɴ⁻¹都是连续的，我们称具有ψɴ这样性质的映射为同胚（homeomorphism），同时也称I和Cɴ同胚。当然，ψɴ是同胚则ψɴ⁻¹必然也是同胚，故I和Cɴ同胚等价于Cɴ和I同胚。

类似地，我们还能定义另外三个半圆以及分别构建它们与I之间的同胚：

东半圆：

西半圆：

南半圆：

显然，东西南北四个半圆覆盖了单位圆C上的所有点，于是对于C上任意一点p，总能找到一个包括p点的半球H与ℝ中的单位开区间I同胚。

图2：圆上的流形

至此，我们就在C上完成了微分体系的初步搭建，这个就是大名鼎鼎的流形（manifold）。

将单位圆从ℝ²升级到三维空间（记为，ℝ³）就得到单位球面，

可以将S分为，东西南北前后，六个半球面，并分别建立它们和ℝ²中单位开圆盘，

之间的同胚。例如：北半球面（记为，Sɴ）为，

同胚（记为，ψɴ：D→Sɴ）可定义为，

相应的逆映射（记为，ψɴ⁻¹：Sɴ→D）则是，

同样是因为六个开半球面构成了S的全覆盖，所以对于S上任意一点p，都存在包括p的一个半球面A与ℝ²中单位开圆盘D同胚，从而我们就在S上搭建了一个流形。

图3：球面上的流形

推而广之，用类似上面的方式，我们可以尝试在任意n维的欧氏空间（记为，ℝⁿ）中的任意点集M上构造流形（虽然不一定成功）。

对比以上构造的流形，

半圆H是ℝ²中某个开集W（取X⁺、X⁻、Y⁺ 、Y⁻ 之一）与C的交 H=W∩C ，单位开区间I是ℝ中的开集；半球面A是ℝ³中某个开集W（取X⁺、X⁻、Y⁺ 、Y⁻、Z⁺ 、Z⁻ 之一）与S的交 A=W∩C，单位圆盘D是ℝ²中的开集；

我们可以归纳总结出一个流形的正式定义如下：

★ 若于是非空点集M⊆ℝⁿ中任意一点p，总有ℝⁿ中包含p的一个开集W，使得W∩M与ℝᵐ中的某个开集V同胚，则称M是一个m维流形。

图4：流形

其中，任意一个同胚 ψ: V→W∩M 称为 区域 W∩M 的一个参数化（parameterization），其逆同胚ψ⁻¹:W∩M→V称为区域W∩M 的一个坐标卡（coordinate chart）。

根据定义★，前面搭建的流形C和S分别是1维流形和2维流形。实际上，更一般的情况是，在ℝⁿ中定义超单位球面，

对于朝向任意坐标轴Xᵢ两个单侧的超半球面

都有

使得其分别同胚于ℝⁿ⁻¹中的超单位开圆盘

这些超半球面全覆盖Sⁿ⁻¹，因此Sⁿ⁻¹是一个n-1维流形。

S¹和S²就是前面搭建的C和S，而S⁰是ℝ¹=ℝ中单位开区间I的两个端点-1和 1， 我们定义0维欧氏空间ℝ⁰为原点0，则常函数ψ⁻(u)=-1和ψ⁺(u)=1分别让-1和1与0同胚。

再看定义★，我们发现：★实质上仅用到 开集 和 连续性（来自同胚） 这两个概念，而连续性其实可以借由开集来定义（>注：我之前有关于连续性的详细回答，大家可以搜索我的主页，这里不再累述），故我们只需要让 M 具有 开集，就可以定义流形了。

具有开集的M称为拓扑空间，因此我们就有了一个新定义：

☆ 若对于Hausdorff拓扑空间M的中任意一点p，总有包含p的一个开集U与ℝᵐ中的某个开集V同胚，则称M是一个m维流形。

同一个点集上可以搭建不同的微分结构，我们完全可以在C上建立另一个：有映射，

将整个ℝ映射到ℝ² 中（记为，Ψ : ℝ→ℝ²）。很显然，Ψ在任意开区间V=(a, b)中的限制，

由于正弦函数 和 余弦函数 都是连续的， 所以Ψ是连续的，进而ψᴠ也是连续的。 我们只要保证区间V的长度小于1，即，b-a<1，则 ψᴠ 就是一一到上的双射，此时ψᴠ的逆映射（记为，ψᴠ : Cᴠ→V），

也是连续的，故此时ψᴠ是同胚。

在ℝ中，所有这些长度小于1的开区间V在对于同胚ψᴠ下的像（记为，Imψᴠ=ψᴠ(V)）构成了对C的一个全覆盖，于是我们在C上就搭建了一个流形。

图6：《高数》名言：“可导一定连续，连续不一定可导！”

连续的曲线（或曲面）可能有棱角，不应是光滑的，这表现在其导函数并不连续，例如：

图7：连续而不光滑

如果一个函数的任意阶导函数（或偏导函数）都是连续的，则称该函数是光滑的（smooth），如果组成向量函数的函数都是光滑的，则该向量函数也是光滑的。称双向光滑的同胚为微分同胚（diffeomorphism）。将★中的同胚升级为微分同胚，我们就得到了 光滑流形（smooth manifold）的定义。

现在，来考察我们建立的第一个同胚的双向光滑性，先看正向：

由于ψɴ的定义域I是开集，没有边界点，故I会不影响其内每个点的各阶导数的存在，而ψɴ的各阶导函数，

显然在I内都是连续的，故ψɴ是光滑的。再看逆向：

虽然 ψɴ⁻¹ 看起来很简单，但是我们却遇到了麻烦：由于 ψ⁻¹的定义域Cɴ是ℝ²中一条曲线，其中任意一点p都是Cɴ边界，于是在Cɴ内p没有偏导数，这使得我们无法考察 ψ⁻¹的光滑性。那么如何解决这个问题呢？我们可以这样：

先在ℝ²中取一个包含p点的开集W，然后建立一个从W到ℝ的映射：

由于Ψ的定义域W是开集，于是不会影响Ψ在p点附近的各阶偏导，而Ψ的各阶偏导函数除了dΨ/dx=1外，其它都是0，显然连续，因此Ψ在p点附近是光滑的。

再将Ψ 和 ψɴ⁻¹ 都限制在W∩Cɴ内，有，

这说明Ψ 和 ψɴ⁻¹ 在W∩Cɴ内是一致的，因此ψɴ⁻¹也在p点附近是光滑。

最后，用以上方法，我们可以验证ψɴ⁻¹在Cɴ内的每一个点p附近都是光滑，进而ψɴ⁻¹在Cɴ是光滑的。

至此，考察完毕，得到结论：第一个同胚是一个微分同胚。实际上，我们可以验证以上建立的所有同胚都是微分同胚，从而以上的流形都是光滑流形。

流形在自然界普遍存在，例如：

水生动物的皮肤，每一块鳞片就是欧氏空间中的一个开集，它总是紧贴皮肤的一块区域，这就构成一个同胚，而鳞片全覆盖皮肤，于是组成流形；全世界现存的每张地图都与地球上的某个区域一一对应，构成同胚，所有地图全覆盖整个地球，构成流形；画家每一刮刀的油彩覆盖画布，一幅油画就是一个流形；房顶被一片片青瓦覆盖，墙面被一块块腻子覆盖，地面被一条条底板覆盖，它们都是流形；甚至你穿着衣的皮囊都是个流形。

所以流形并不陌生，只是大家平常意识不到罢了。

——[END]——

本文内容由快快网络小馨创作整理编辑！