关于高次方程的著作(关于高次方程求解的论文)

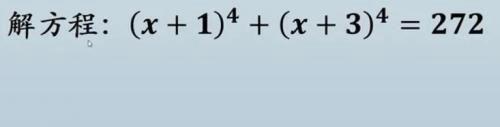
导语：关于高次方程（x+a）^4+（x+b）^4=C（a、b、c为常数）解法的探讨

解法-、

分析：∵根据杨辉三角（a+b）^4=a^4+4a^3b+6a^2b^2+4ab^3+b^4…①

（a-b）^4=a^4-4a^3b+6a^2b^2-4ab^3+b^4…②

∴①+②得：

（a+b）^4+（a-b）^4=2（a^4+6a^2b^2+b^4）

∵x+1+x+3/2=x+2

∴令x+2=a 则x+1=a-1，x+3=a+1，

∴原方程可化为（a-1）^4+（a+1）^4=272

∴2（a^4+6a^2+1）=272

a^4+6a^2+1=136

即a^4+6a^2-135=0

（a^2-9）（a^2+15）=0

∴a1=3，a2=-3

当a=3时， x+2=3 ， x=1

当a=-3时，x+2=-3， x=-5

∴原方程的解为：x1=1，x2=-5

解法二、

从数字272入手

∵1^4=4，2^4=16，3^4=81，4^4=256

∴272=256+16=4^4+2^2

∴原方程可变为：

（x+1）^4+（x+3）^4=4^4+2^4

∴[（x+1）^4-2^4]+[（x+3）^4-4^4]=0

[（x+1）^2+2^2][（x+1）^2-2^2]+[（x+3）^2+4^2][（x+3）^2-4^2]=0

（x^2+2x+5）[（x+1）+2][（x+十1）-2]+（x^2+6x+25）[（x+3）+4][（x+3）-4]

（x^2+2x+5）（x+3）（x-1）+（x^2+6x+25）（x+7）（x-1）=0

（x-1）（x^3+2x^2+5x+3x^2+6x+15+x^3+6x^2+25x+7x^2+42x+175）=0

（x-1）（2x^3+18x^2+78x+190）=0

（x-1）（x^3+9x^2+39x+95）=0

（x-1）（x+5）（x^2+4x+19）=0

∴x1=1 x2=-5

解法三、原方程做如下变形：

（x^2+2x+1）^2+（x^2+6x+9）^2=272

令x^2+4x+5=a

∴x^2+2x+1=a-2x-4，x^2+6x+9=a+2x+4

再令2x+4=b

∴（a-b）^2+（a+b）^2=272

∴a^2+b^2=136

∴（x^2+4x+5）^2+（2x+4）^2=136

[（x+2）^2+1]^2+4（x+2）^2-136=0

（x+2）^4+6（x+2）^2-135=0

∴[（x+2）^2+15][（x+2）^2-9]=0

∵（x+2）^2+15=0，不成立

∴只有：（x+2）^2-9=0

[（x+2）+3][（x+2）-3]=0

∴x1=-5，x2=1

本文内容由快快网络小琪创作整理编辑！