三种不同的换元法解方程题(三种不同的换元法解方程怎么解)

导语：三种不同的换元法解方程

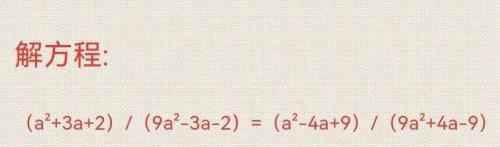
解法①：原方程等式左右x9变为：

（9a²+27a+18）/（9a²-3a-2）=（9a²-36a+81）/（9a²+4a-9）

[9a²+9（3a+2）]/[9a²-（3a+2）]=[9a²-9（4a-9）]/[9a²+（4a-9）]

令9a²=x，3a+2=y，4a-9=z

∴（x+9y）/（x-y）=（x-9z）/（x+z）

∴（x+9y）（x+z）=（x-y）（x-9z）

x²+xz+9xy+9yz=x²-9xz-xy+9yz

∴10xz+10xy=0

∴xz+xy=0

∴x（y+z）=0

∴x=0或y+z=0

当x=0时，9a²=0，∴a=0

当y+z=0时，3a+2+4a-9=0，∴a=1

∴经验根，原方程的解为:a1=0，a2=1

解法②:令3a+2=x，4a-9=y

∴（a²+x）/（9a²-x）=（a²-y）/（9a²+y）

∴（a²+x）（9a²+y）=（a²-y）（9a²-x）

∴9a⁴+a²y+9a²x+xy=9a⁴-a²x-9a²y+xy

（a²x+a²y）+（9a²x+9a²y）=0

a²（x+y）+9a²（x+y）=0

∴10a²（x+y）=0

∴10a²=0或x+y=0

当10a²=0时，a=0

当x+y=0时，即3a+2+4a-9=0，a=1

∴经验根，原方程的解为:a1=0，a2=1

解法③：i）依题意a=0是原方程的解。

ii）a≠0，原方程变为

（1+3/a+2/a²）/（9-3/a-2/a²）=（1-4/a+9/a²）/（9+4/a-9/a²）

令3/a+2/a²=x，4/a-9/a²=y

∴（1+x）/（9-x）=（1-y）/（9+y）

∴（1+x）（9+y）=（9-x）（1-y）

∴9+y+9x+xy=9-9y-x+xy

∴10x+10y=0

∴x+y=0

∴3/a+2/a²+4/a-9/a²=0

∴3a+2+4a-9=0

∴a=1

∴经验根，原方程的解为:a1=0，a2=1

本文内容由小馨整理编辑！