初中找等量关系的小窍门(初中数学等量关系式大全)

如图所示，在梯形ABCD中，AB=3，BC=4，CD=2，DA=1，求此梯形面积。

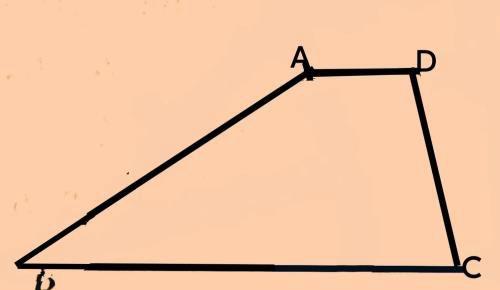
解析：我们知道梯形的面积公式为：

S梯=(上底+下底)x高/2。

现在已经知道了两底的长分别为：AD=1，BC=4，

如果能求出高，

则此题可解。

不管三七二十一，

先将高线作出来，

过A点作AH⊥BC，

交BC与点H，

如下图所示。

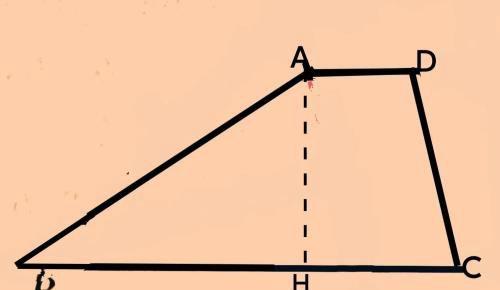
又由已知条件可知，AB=3，

而BC-AD=4-1=3，

与AB有等量关系，

那么在BC上取一点E，

使CE=AD即可，

或过A点作AE∥DC亦可，

此时四边形ADCE为平行四边形，

且BE=3，AE=CD=2，

并可获知△ABE为等腰三角形，

如下图所示。

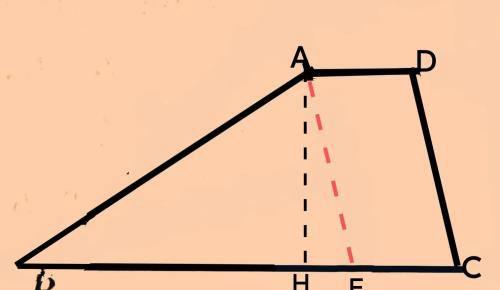
由图可知，AH也是△ABE的高，

则S△ABE=AH·BE/2，

又在等腰△ABE中，过B点作底边的高线BF，如下图所示，

则BF=√BE²-EF²=√9-1=2√2，

所以S△ABE=BF·AE/2

=2√2x2/2=2√2，

所以AH·BE/2=2√2，

所以AH=4√2/3，

所以S梯ABCD=【(1+4)x4√2/3】/2

=10√2/3。

小结:对于本题，通过线段之间的数量关系，构造出等腰△ABE是关键。

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请与我联系，一经查实立刻删除内容。本文内容由快快网络小思创作整理编辑！