利用坐标证明一道竞赛几何题的方法(坐标法证明几何问题)

导语：利用坐标证明一道竞赛几何题

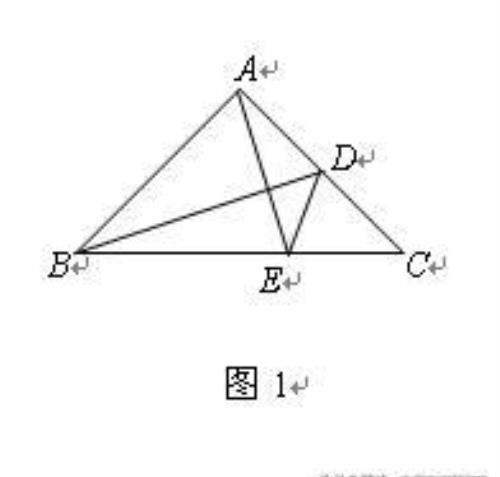
题：如图1，等腰Rt△ABC中，AB=AC，∠BAC=90°，D是AC的中点，AE⊥BD交BC于E．

求证：∠ADB=∠CDE．

分析：从几何的角度出发进行证明虽然有点难度，但也并非是无从下手．由已知，图中有相等线段AB=AC，AD=DC，因此自然会想到构造三角形全等．注意到△ABD与△ACE，它们虽然不全等，但有AB=AC，∠DBA=∠CAE，因此，在△ACE基础上构造与△ABD全等的三角形．

证明：过点C作CF⊥AC交AE延长线于点F（如图2）．

因为∠BAC=90°，AE⊥BD，

所以∠ABD=∠CAF，

因为AB=AC，∠BAD=∠ACF，

所以△ABD≌△CAF，

所以AD=CF，∠ADB=∠F．

因为AD=CD，

所以CD=CF，

因为△ABC是等腰直角三角形，

所以∠DCE=45°，

所以∠FCE=90°-45°，

所以∠DCE=∠FCE，

又CE=CE，

所以△CDE≌△CFE，

所以∠CDE=∠F，

所以∠ADB=∠CDE．

如果考虑到△ABC是直角三角形，把它放进直角坐标系中，通过点的坐标容易沟通各边之间的关系，再通过三角函数便可以达到证明∠ADB=∠CDE ．

证明：如图3，以点A为原点O，直线AC、AB分别为x轴、y轴建立直角坐标系．

设AB=AC=2a，则点B(0，2a)，C(2a，0)，D(a，0)，

在Rt△ABD中，

tan∠ADB=AB/AD =2；

设直线BC的解析式为y=kx+2a，

把点C的坐标代入，得

0=2ak+2a，解得k=-1，

所以直线BC的解析式为y=-x+2a；

设直线BD的解析式为y=mx+2a，

把点D的坐标代入，得

0=am+2a，解得m=-2，

所以直线BD的解析式为y=-2x+2a；

因为直线AE与BD垂直，

所以直线AE的解析式为y=1/2·x.

联立直线BC、AE的解析式：y=-x+2a和y=1/2·x，

解得x=4a/3，y=2a/3，

所以交点E的坐标为(4a/3，2a/3)，

作EF⊥x轴于点F．则

EF=2a/3，

DF=AF–AD=4a/3-a=a/3，

在Rt△DEF中，

tan∠EDF=EF/DF=2a/3÷a/3=2，

所以tan∠ADB=tan∠EDF，

所以∠ADB=∠CDE．

运用坐标证明几何题思路清晰，方法简便，但美中不足的是过程运算较繁杂．

本文内容由快快网络小楠创作整理编辑！