多边形面积的知识(多边形面积计算知识点)

导语：多边形的面积复习（二）

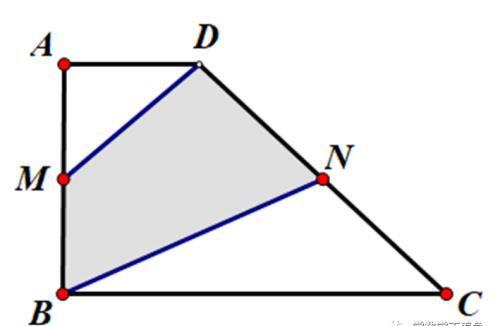
3、如图，在四边形ABCD中，M为边AB的中点，N为边CD的中点，四边形ABCD的面积是80平方厘米，则四边形BNDM的面积是（ ）平方厘米。

这个阴影部分是个不规则图形，想用割补法来做，可是题中除了四边形ABCD的面积是80平方厘米，其他没有什么底啊、高啊的数据，所以此路不通。

“M为边AB的中点，N为边CD的中点”，以前有过类似的题，都有“什么等底等高，然后面积相等的”，那么画一条连接BD的辅助线，如下图：

从图中可以看出：三角形AMD（①)和三角形MBD（②），这两个三角形等底等高，所以面积相等。

同样，三角形BND（③）和三角形BCN（④），这两个三角形等底等高，面积也相等。

综上所述，四边形BNDM（②+③）=①+④,四边形BNDM的面积就是四边形ABCD的一半，四边形BNDM面积＝80÷2=40平方厘米。

4、一个等腰直角三角形，它的腰长是6厘米，它的面积是（ ）平方厘米。一个长41厘米，宽30厘米的长方形最多可以剪（ ）个这样的三角形。

前面讲过类似的题目，如果还用大面积除以小面积，那肯定错了！

41×30÷（6×6÷2）=68（个）……6（平方厘米），请看下图，能剪这么多么？

有学生说，老师应该用41÷6=6……5，30÷6=5，6×5×2=60（个），这种方法只能剪60个三角形。

可是，再看看下面这幅图：

计算后得出a=18的平方根≈4.243，下图中的AB≈16.97,AB<17，CD≈29.70，CD<30。

最后，一共可以剪67个三角形。当然，这种答案、解法非常坑，对于小学生来说，这种题目没有什么价值。

正常的题目都是大长÷小长，大宽÷小宽；或者是大长÷小宽，大宽÷小长啦！

小贴士：遇到此类题目，千万不能再用大面积除以小面积啦！

本文内容由快快网络小嫣整理编辑！