2个圆的交点怎么求(两圆包含的条件)

一道高中题-求包含两个相交圆的公共圆的半径

求一个圆的最小直径，要求它能够将圆

和圆

包含在内部。

解：同时包含两个不同圆的圆，一定是两个圆的公切圆， 如图，画出示意图，

下面打算用两种方法解这道题，一种方法是通过直线MN的方程求出直线与两个圆的交点坐标， 然后根据两点间的距离公式求出大圆MN的直径，然后半径即可得出。

另一种方法是结合几何的运算。

方法1： 圆O的圆心为（0， 0），其半径为1， 圆P的半径为2， 圆心为（1，2）

因此直线PO的方程为y=2x, 将其延长与两个圆的交点就是M和N， 且MN是大圆的直径，这是因为以MN为直径，以MN中点为圆心的圆与给定的两个圆相切，因此MN就是所求圆的直径。将y=2x 带入：

得出N的坐标， x=-1/√5, y=-2/√5

同样将y=2x带入

得出M点的坐标， x=1+2/√5, y=2+4/√5

利用两点之间的距离公式得出MN=3+√5

所以所求圆的半径为（3+√5）/2

方法2： 如图所示，

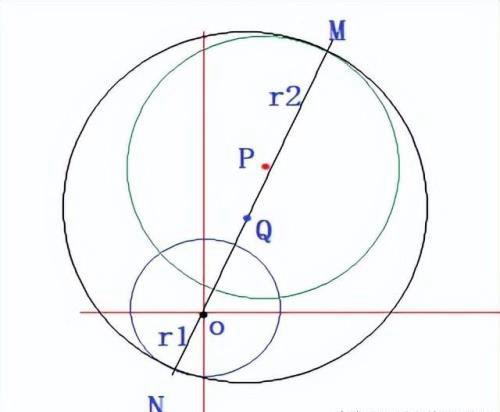
设Q是外切圆的圆心，并设其半径为R，O和P分别是已知圆的两个圆心，

显然OP很容计算出

OP=√5

但OP=OQ+QP

=R-r1+R-r2

这样R=(OP+r1+r2)/2=(√5+1+2)/2=(√5+3)/2

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请与我联系，一经查实立刻删除内容。本文内容由快快网络小冰创作整理编辑！