直角坐标系中的几何问题(直角坐标系里的三角函数)

导语：中考进阶 几何与函数 05 直角坐标三大公式 中点坐标 两点 点到直线距离

中考进阶 几何与函数05 直角坐标三大公式 中点坐标 两点 点到直线距离

〖坐标基本原理〗

[1]. 与x轴平行的直线上的点，纵坐标不变；

[2]. 与y轴平行的直线上的点，横坐标不变。

〖中点坐标公式〗

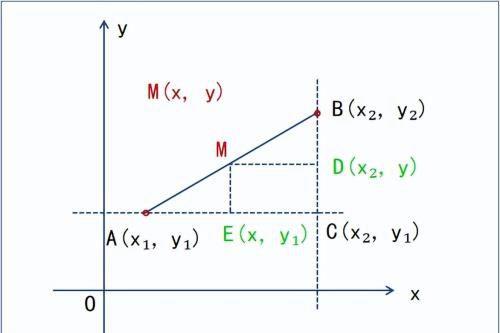
已知A(x₁, y₁)、B(x₂, y₂)，M是AB的中点，求M(x, y)。

作AC∥x轴、BC∥y轴，二者相交于点C；设D是BC中点，E是AC中点；

由坐标基本原理，易得：

C(x₂, y₁)

D(x₂, y)

E(x, y₁)

∵D是BC中点，∴BD/DC＝1，即

(y₂－y)/(y－y₁)＝1

解得

y＝(y₂＋y₁)/2；

同理，解得

x＝(x₂＋x₁)/2；

〖两点距离公式〗

已知A(x₁, y₁)、B(x₂, y₂)，求|AB|。

如图：

|AC|＝|x₂－x₁|，|BC|＝|y₂－y₁|，

由勾股定理 |AB|²＝|AC|²＋|BC|²，即

|AB|＝√[(x₂－x₁)²＋(y₂－y₁)²]

〖点到直线距离公式〗

已知：

直线L y＝kx＋b，

点P坐标P(m, n)，

求点P到直线L的距离d。

我们用垂线法，诱导这个公式。

垂线法

互相垂直的直线斜率互为负倒数，可求得垂线PD所在直线方程(k≠0)：

PD所在直线：y＝-(1/k)(x－m)＋n

与 y＝kx＋b联立求解交点（垂足），得垂足D的坐标：

x₁＝(m＋kn－kb)/(1＋k²)

y₁＝(km＋k²n＋b)/(1＋k²)

△x＝x₁－m＝-k(km－n＋b)/(1＋k²)

△y＝y₁－n＝(km－n＋b)/(1＋k²)

由两点距离公式，得

PD＝d＝√[(△x)²＋(△y)²]

＝|km－n＋b|/√(1＋k²)

结论：

将L的函数表达式写成方程的形式：kx－y＋b＝0

P点到直线L的距离d，等于将P点坐标代入直线方程(km－n＋b)计算结果的绝对值，再除以√(1＋k²)。

结论很整洁，也很有用。

初中未必讲，但原理上没有一点难度。

垂直直线的斜率互为负倒数，已经在《中考进阶 几何与函数 02 直角坐标系中 两直线的位置关系 平行与垂直》介绍过，也是很有用的公式。

本文内容由小纳整理编辑！