实数的可排序性是什么(实数的可排序性例题)

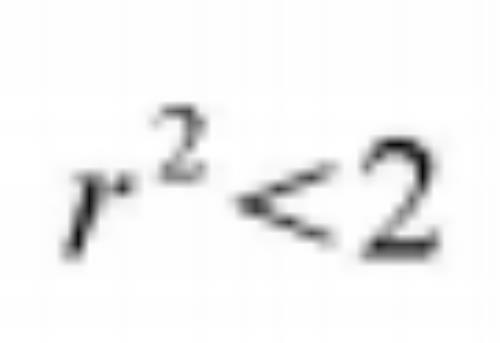
导语：实数的可排序性

如果两个数都是有理数，由于有理数的可列性，则这个问题在算术中已经解决。

如果说 α1 是无理数，而 α2 是有理数，则问题也马上得到解决: α1 是集合R 的某个分割的界限，根据界限的定义本身我们说 α2<α1 或者 α2>α1 取决于有理数 α2 属于此分割的A类或B类.

这里解释一下一个无理数可以对实数集进行分割的概念：

我们首先在有理数中(对我们来说任何其他的数暂时还不存在)找这样的数，它的平方等于数2 ，且容易发现，这种(有理)数不存在，这就表明:无论我们选择什么样的有理数，我们都将有

都小于B 类的每一个数.现在很明显的是，如果我们把零和一切负(有理)数都归入A类，上述结论不会改变.此时我们将得到将整个集合R 分为A和B两类的一个分割，同时A类的每一个数都小于B 类的每一个数.我们约定，若将集合分成两个非空的类[即每一个类中至少包含有一个数] (A ,B)，而使A 类中的每一个数都小于B类中的任意数，就称它是一个割(确切地说是集合的分划) .我们因此也得到了集合R 的某个确定的分割.

最后，设数 α1 和α2 是两个无理数.因为这两个数互不相同，则以它们为界限的那两个分割也互不相同.

先解释一个无理数可以对实数集进行分割：

特别地，这两个分割的左边的类A1和A2 也互不相同.这就表明在这些集合中的某一个，例如A2，可以找到这样一个有理数 r是在 A1中所没有的.

从r不属于A1，得出

两种情形之一一定应当成立。

本文内容由快快网络小姿创作整理编辑！