求两个三角形的面积差(两个三角形面积公式是怎样)

导语：一道初中几何题-求两个三角形的面积之比

一道初中几何题-求两个三角形的面积之比

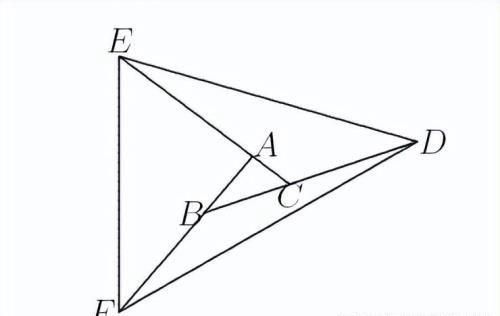
在下面的图中并不是按比例绘制的，BD = 2BC，CE = 3CA, AF = 4AB。求三角形DEF与三角形ABC的面积比是多少 ？

解：方法1-初中解法

这是一道非常简单的图形计算题，利用等高三角形的面积之比等于其底边之长的比值，如图，做出BE和AD的连线，若设三角形ABC的面积为S， 那么根据EA/AC=2:1, 则三角形ABC的面积为2S， 同样其相邻的三角形BEF的面积为6S，其它的内部三角形的面积计算方法与此相似，已经标在了相应的三角形的内部，这样三角DEF的面积为所有的小三角形的面积之和，所以三角形DEF的面积A=18S， 因此三角形DEF与三角形ABC的面积之比为18:1.

方法2-高中解法

这里要用到一个三角形的面积公式S=ab/2(sinα)

三角形AEF与三角形ABC有相邻的互为补角，且有sin(180°-α)=sinα，

这样相邻的三角形面积之比就变成边长的乘积之比

若设三角形ABC的面积为1， 那么红色的三角形AEF的面积=8，

绿色三角形CDE的面积=3，

黄色三角形BDF的面积=6

所以DEF的面积=8+3+6+1=18

因此最后求的两个三角形的面积之比为18:1

本文内容由快快网络小迪创作整理编辑！