从二项式定理到多项式定理的公式(二项式定理多项式怎么求)

今天来说说二项式定理与多项式定理。

二项式定理是多项式乘法法则（基于乘法分配律）的推广，最早由牛顿给出，莱布尼茨在此基础上给出了多项式定理（在这里两人仍要争斗一番）。

首先，我们知道多项式乘法法则：

现在我们来研究二项式展开的各项：由于是n个(a+b)相乘,每个(a+b)在相乘时有两种选择,选a或b,而且每个(a+b)中的a或b都选定后,才能得到展开式的一项。因此,由分步乘法计数原理可知,在合并同类项之前,的展开式共有2n项,其中每一项都是的形式。对于某个k(k=0,1,…,n),对应的项是由nーk个(a+b)中选a,k个(a+b)中选b得到的。由于b选定后,a的选法也随之确定,因此,出现的次数相当于从n个(a+b)中取k个b的组合数.这样,的展开式中,共有个,将它们合并同类项,就可以得到二项展开式：

这便是二项式定理。

的展开式共有n+1项,式中的叫做二项展开式的通项。

上述二项式定理还可以简记为：

二项展开式的系数规律，早在北宋时我国数学家贾宪就已发现，遗憾的是其著作佚失，但其主要内容被杨辉的著作《详解九章算法》(1261)所抄录，因此传世，该书中的“开方作法本源”图，注明“贾宪用此术”。这就是著名的“贾宪三角”，或称“杨辉三角”。

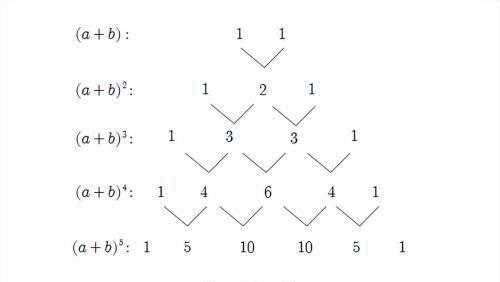
在欧洲，帕斯卡（1623-1662）在1654年发现这一规律，所以这个表又叫做帕斯卡三角形。后来牛顿于1664年、1665年间提出了一般形式的二项式展开公式，并推广到有理数指数的情形。18世纪，瑞士的欧拉和意大利的卡斯蒂隆又分别推广了实数指数情形的二项式定理。

我们再来看看莱布尼茨的多项式定理：

这个展开式的通项该如何确定呢？

这个式子由n个因式相乘而成的,每个在相乘时都有m个选择,选a₁或a₂或…,而且每个因式中的a₁或a₂或…都选定后,才能得到展开式的一项。因此,由分步乘法计数原理可知,在合并同类项之前,展开式共有项，其中每一项都是形如：

(n₁+n₂+…+=n且n₁,n₂,…是非负整数).

项可以看成：在n个因式中首先任取出n₁个因式,而在这n₁个因式中都是选择a₁,然后再从剩下的(n-n₁)个因式中任取出n₂个因式,而在这n₂个因式中都是选择a₂,…最后从剩下的个因式中都选择相乘而来的。这样项

出现的次数就是它的系数。

因为

因而展开式的通项为

上式中n₁+n₂+…+=n且n₁,n₂,…是非负整数，这个公式叫做多项式定理，它是二项式定理的推广。

多项式定理的本质其实是次数的分配。的展开式就是把次数n分配给每一个a(由于可以分得0次方,所以每个a分到的次数是非负整数).

现在思考的展开式共有多少项？(合并同类项后)。

这就相当于求不定方程n₁+n₂+…+=n有多少组非负整数解。这是排列组合中的隔板法模型。等价于不定方程 x₁+x₂+…+=n+m ①(其中xi=ni+1 ,i=1,2,…)有多少组正整数解。现设想(n+m)个无区别的小球依次摆放在一条直线上,从(n+m)个小球产生的(n+m-1)个间隔中,插入(m-1)个隔板,把小球分成m份,依次为x₁,x₂,…,个。这时,每一种插入法都对应不定方程①的一组正整数解。而这时的插入法数是,从而不定方程①的正整数解的组数是,所以 展开式中共有项。

下面举例说明多项式定理在高中数学中的应用(当然最有意义的应用就是计算三项式的展开，毕竟二项式的展开用二项式定理就可以了)：

例1:的展开式中x³项的系数是多少？

解：本题可以理解为将次数5分配给括号中的3个子项(每项分得非负整数次数且次数之和为5)。设给第一项分得m次，第二项分得n次，要最终形成x³项,则2m+n=3,该方程的非负整数解有两组：

当m=1,n=1时,也就是给第一项和第二项都分配1次,给第三项分配3次,这样产生的系数是:

当m=0,n=3时,也就是给第一项分配0次,给第二项分配3次,给第三项分配2次,这样产生的系数是:

这两个系数加,40+(-80)=-40,所以x³项的系数是-40。

例2:的展开式合并同类项后共有多少项？

解:本题相当于将次数10分配给括号中的5个子项(每项分得非负整数次数且次数之和为10),等价于求不定方程 x₁+x₂+x₃+x₄+x₅=10 的非负整数解的组数,等价于求 y₁+y₂+y₃+y₄+y₅=15(yi=xi+1) 的正整数解的组数。可以理解为在15个排成一排的无区别的小球中间形成的14个间隔中插入4个隔板,把小球分成5份,每一种插入法对应一组解,从而解的组数是

组,所以上述展开式合并同类项后共有1001项。

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请与我联系，一经查实立刻删除内容。本文内容由快快网络小玥创作整理编辑！