两个圆有什么关系(两个圆有几种不同的位置关系)

导语：公务员考试行测备考：论两个圆的重要性

在数量关系考试中，容斥问题总是有着七十二变，让考生有种丈二和尚摸不着头脑的感觉，无从下手。为了帮助大家攻克这一难题，我们今天主要从容斥问题中的二集合题型入手为大家解惑。

在容斥问题中的解决方法中，画图法是非常实用的方法，可以清晰明了的解答出准确答案。

在解答容斥问题时，首先要明确题目特征，即当题目中出现“符合A条件，符合B条件，都符合或者都不符合”的字眼，可判定此题为二集合容斥问题;其次确定条件A、B的具体内容，而对于一些未明确给出相应集合条件内容的题目，考生们需要认真审题，根据“都”或者“都不”而进行确定。接下来即可通过画图法解题，基本步骤如下：

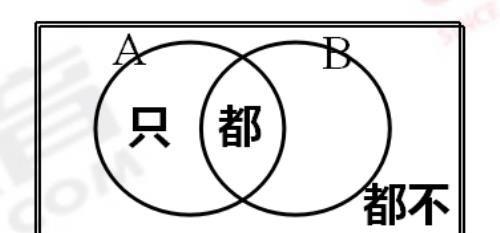
1、画图：注意“都”，两个圆通过部分重叠画出;若出现“都不”，需要在圈外加框;

2、标数：对应数字标在图中相应的地方，此处应注意“只”部分，要标注在圈内;(见图)

3、求和：总和=A+B+都不-都(不存在“只”)。

接下来我们通过两道例题实践了解一下，帮助大家学习吸收此法。

【例1】现有50名学生都做物理、化学实验,如果物理实验做正确的有40人, 化学实验做正确的有31人, 两种实验都做错的有4人, 则两种实验都做对的有( )人。

【例2】某委员会有成员465人，对2个提案进行表决，要求必须对2个提案分别提出赞成或反对意见。其中赞成第一个提案的有364人，赞成第二个提案的有392人，两个提案都反对的有17人。问赞成第一个提案且反对第二个提案的有( )人。

此两道例题的题目中均出现“都或都不”的情况，我们分别来具体分析一下。例1中包含两种情况正确的人数，出现“都对和都错”，即出现“都不”的情况，第一步画图应有框，第二步标数时没有“只”。具体的情况考生可参考图1.

通过求和可列出等式：40+31+4-x=50，解出都对的人数为25人。这样的运算的过程是不是既简洁又准确呢?相信你们能够很快掌握此法的。接下来看一下例2.

例2中出现“两个提案都反对”，没有“都不”，即作图时应该是没有框的。此题关键在于确定两个集合的具体内容，根据“都反对”确定条件A、B分别是“反对第一个提案为465-364=101人”与“反对第二个提案465-392=73人”，进而通过标数即可得到“赞成第一个提案且不赞成第二个提案的人数为73-17=56人”。

此题通过画图法可以清晰的得到答案，避免马虎的情况出现。

这就是两个圆的奥秘，考生们学会了吗?正所谓细节决定成败，考生要注意“三步走”中的每个细节，进而准确作答二集合容斥问题。

本文内容由快快网络小故创作整理编辑！