在实数轴上稠密(数轴具有什么样的性质)

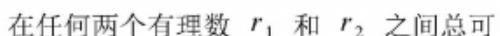
导语：数轴的稠密性

任何两个有理数之间存在无穷多个有理数：

同理，一个有理数和一个无理数之间存在无穷多个无理数。

两个有理数之间存在无穷多个无理数：

把根号2换成根号p,p为非完全平方数，即得无穷多个。

两个无理数之间存在无穷多个有理数：

先介绍阿基米德性质。

阿基米德性质可以认为以下二句叙述的任一句：

给出任何数，你总能够挑选出一个整数大过原来的数。给出任何正数，你总能够挑选出一个整数其倒数小过原来的数。

这等价于说，对于任何正实数a、b，如果 a<b，则存在自然数n，有na>b,即

上述性质可以认为是公理。

现在假设y-x<1，则根据阿基米德性质，有n(y-x)>1,n为自然数。由于ny和nx之间的间隔大于1，所以两者之间必然包含一个整数，假设这个整数是m,则存在关系nx<m<ny,也就是

而m/n是有理数，再取半操作重复应用，所以得到两个无理数之间存在无穷多个有理数。

综合上述内容，数轴上任意两个数（包括有理数和无理数）之间，包含了无穷多个其它的数字（同样包括有理数和无理数），所以数轴是稠密的。

本文内容由快快网络小鸣创作整理编辑！