圆弧对应的圆心角和圆周角的面积关系(圆周角圆心角的综合应用题)

导语：圆弧、圆周角及圆心角应用题5例

圆弧、圆周角及圆心角应用题5例

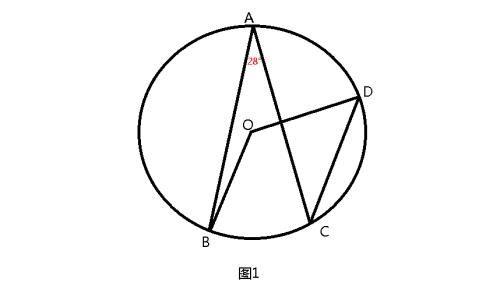
题目1：如图1，点A、B、C、D在圆O上，OB∥CD，若∠A=28°，则∠BOD的度数为（124°）。

解题思路：图2，连接OB、OC，

∵OB∥CD， OC=OD，∴∠BOC=∠OCD=∠ODC。

又∵∠A=28°，∴∠BOC=2x28°=56°。

∠BOD=∠BOC+（180°-∠OCD-∠ODC）=180°-∠BOC

=180°-56°=124°。

题目2：在圆O中，弦AB垂直弦CD，AE是直径，求证:弧BC=弧DE。

解题思路：图2，连接AC、AD、DE，欲证明弧BC=弧DE，转化成证明其对应的圆周角相等就行了。

利用已知条件及直径所对的圆周角=90°，很容易证明两段弧所对的圆周角相等（见图2中标示）。

题目3：如图1，点A、B、C在圆O上，BC=6，∠BAC=30°，则圆O的半径为（6）。

解题思路：图2，连接OB、OC，则圆心角=60°，△OBC为等边三角形，故半径=BC=6。

题目4：如图，AB是圆O的直径，C是圆周上一点，劣弧AC以线段AC为对称中心翻转与AB相交于点D，已知∠BAC=25°，求∠DCA的大小（40°）。

解题思路：如图2，弧AC所对的圆周角为65°，翻转弧AC所对的圆周角为∠DAC+∠DCA同样为65°，故∠DCA=65°-25°=40°。

本题因CD、CB为等弦亦可证明。

题目5：如图1，已知半径为R的圆O及弦AB，P为圆O上任意一点，PA、PB分别交AB的中垂线于E、F。求证OE·OF=R²。

解题思路：连接OA、OB（图2），欲求证OE·OF=R²，找出相似三角形（母子相似）应该是正确的策略。

因AB⊥OE，M点为劣弧AB的中点，∠α=弧AM度数。

∠EPB=∠PAB+∠ABP，亦等于弧AM度数。

故∠EPB=∠α，∠E=∠OBP，△OBF∽△OEA。

OE/OB=OA/OF,即OE/R=R/OF，

OE·OF=R²成立。

如果再连接OP（R），就是经典的母子相似三角形模型。

本文内容由小春整理编辑！