确定性关系是函数关系相关关系的确定是怎样的(确定的函数关系是相关关系吗)
导语:确定性关系是函数关系,相关关系的确定是怎样确定的呢?
变量的相关性
(1)会作两个有关联变量的数据的散点图,会利用散点图认识变量间的相关关系.
(2)了解最小二乘法的思想,能根据给出的线性回归方程系数公式建立线性回归方程.
回归分析
了解回归分析的基本思想、方法及其简单应用.
知识点详解1.相关关系
当自变量取值一定时,因变量的取值带有一定的随机性,则这两个变量之间的关系叫做相关关系.即相关关系是一种非确定性关系.
当一个变量的值由小变大时,另一个变量的值也由小变大,则这两个变量正相关;
当一个变量的值由小变大时,而另一个变量的值由大变小,则这两个变量负相关.
【注意】相关关系与函数关系的异同点:
共同点:二者都是指两个变量间的关系.
不同点:函数关系是一种确定性关系,体现的是因果关系;而相关关系是一种非确定性关系,体现的不一定是因果关系,可能是伴随关系.
2.散点图
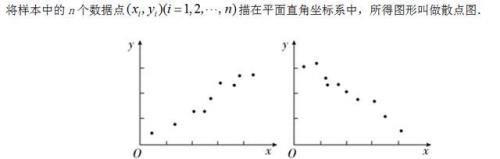
从散点图上看,点散布在从左下角到右上角的区域内,两个变量的这种相关关系称为正相关,点散布在从左上角到右下角的区域内,两个变量的相关关系为负相关.
具有正相关关系的两个变量的散点图如图1,具有负相关关系的两个变量的散点图如图2.
3.回归分析
如果散点图中点的分布从整体上看大致在一条直线附近,则这两个变量之间具有线性相关关系,这条直线叫做回归直线.
回归直线对应的方程叫做回归直线方程(简称回归方程).
4.回归方程的求解
5.相关系数
(1)样本相关系数r的计算公式
6.非线性回归分析
对某些特殊的非线性关系,可以通过变量转换,把非线性回归问题转化成线性回归问题,然后用线性回归的方法进行研究.
在大量的实际问题中,所研究的两个变量不一定都呈线性相关关系,当两变量y与x不具有线性相关关系时,要借助散点图,与已学过的函数(如指数函数、对数函数、幂函数等)的图象相比较,找到合适的函数模型,利用变量代换转化为线性函数关系,从而使问题得以解决.
7.刻画回归效果的方式
考向分析考向一 相关关系的判断
考向二 线性回归方程及应用
考向三 非线性回归方程及应用
求非线性回归方程的步骤:
1.确定变量,作出散点图.
2.根据散点图,选择恰当的拟合函数.
3.变量置换,通过变量置换把非线性回归问题转化为线性回归问题,并求出线性回归方程.
4.分析拟合效果:通过计算相关指数或画残差图来判断拟合效果.
5.根据相应的变换,写出非线性回归方程.
免责声明:本站部份内容由优秀作者和原创用户编辑投稿,本站仅提供存储服务,不拥有所有权,不承担法律责任。若涉嫌侵权/违法的,请反馈,一经查实立刻删除内容。本文内容由快快网络小玥创作整理编辑!