概率论与数理统计之随机变量的独立性问题方法(随机变量的独立性例题)

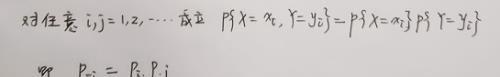
导语：概率论与数理统计之随机变量的独立性问题方法总结

随机变量的独立性：如果对任意x,y都有P{X<=x,Y<=y}=P{X<=x}P{Y<=y}，即F(x,y)=Fx(x)Fy(y)，则称随机变量X与Y相互独立。

随机变量相互独立充要条件：

（1）离散型随机变量X和Y相互独立的充要条件：

离散型随机变量相互独立的充要条件

（2）连续型随机变量X和Y相互独立的充要条件：

连续型随机变量相互独立的充要条件

题型一：离散型随机变量相互独立的判定

例1：

解题思路：本题先求出联合分布，在判断独立性时，若联合分布有零元，但边缘分布不全为零，则随机变量不独立。

解：由题意得：

题型二：连续性随机变量独立性得判定

例2：

解题思路：先求出边缘密度函数，再利用f(X,Y)是否等于边缘密度函数的乘积。

解：由题意得：

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请反馈，一经查实立刻删除内容。本文内容由快快网络小涵创作整理编辑！