在数轴表示无理数的方法

导语：在数轴上表示或辨认无理数

一、实数与数轴上的点的关系：

实数与数轴上的点是一一对应的，它包含两层意思：

① 数轴上的每个点都可以用一个实数来表示；

② 每个实数都可以在数轴上找到表示它的点 。

二、在数轴上画表示无理数的点

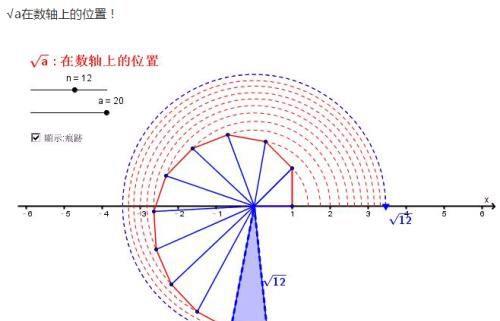
要想在数轴上画出表示无理数的点，需先得到长度为无理数绝对值的线段。

一般地，先根据勾股定理，构造直角三角形得到长度为无理数的绝对值的线段，再以原点为圆心，上述线段长为半径作弧，弧与数轴的交点，便是表示无理数的点 。

注：若无理数为正数，则作弧与数轴正半轴相交；若无理数为负数，则作弧与数轴负半轴相交。

三、在数轴上表示或辨认无理数

例题、利用构造直角三角形和画弧的方法在数轴上找到表示 √2 的点 A；

试利用这个方法，在数轴上找出表示 -√13 的点 B.。（保留作图痕迹）

解：如图所示：点 A 、B 即为所求作的点。

例题图

在数轴上作出表示无理数的点的步骤：

（1）利用勾股定理拆分出哪两条线段长度的平方和等于所画线段（斜边）长度的平方；

（2）以数轴的原点为直角三角形斜边上的一个端点，构造直角三角形；

（3）以数轴的原点为圆心，斜边长为半径画弧，即可在数轴上找到表示该无理数的点。

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请反馈，一经查实立刻删除内容。本文内容由快快网络小珊创作整理编辑！