利用四点共圆证明几何题(证明四点共圆的原理是什么爱问知识人)

欢迎关注：“黔中初数张文松”！

本文为你分享一道，证明四点共圆，在应用 圆周角定理证明动点的轨迹，从而求线段的最小值的题目。

一、题目：

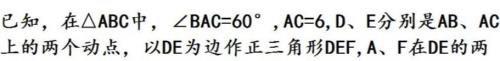
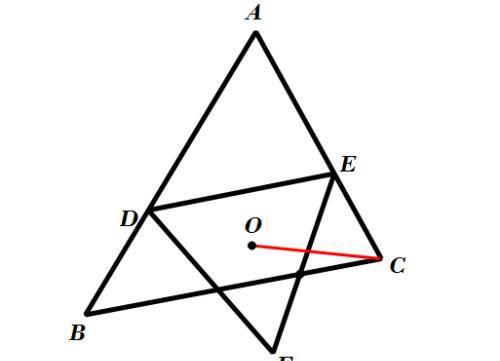
二、分析：

本题中的动点较多，有D、E、F、O四个，主动点D、E，从动点F、O，似乎问题复杂，欲求CO的最小值，首先得知道动点O的运动轨迹是什么，解答数学题，有时也需要大胆猜想，结合图形猜想：点O在∠BAC的角平分线上。猜想是否正确？结合图形试着连接EO、AO,发现∠OED=30°，如果∠OAB=∠OED=30°，那么猜想就是正确的。再结合图形，∠OAB与∠OED所对的一条公共边是OD,然后，又想到连接DO,观察∠OAB与∠OED的位置，只要能证明点A、D、O、E四点共圆即可。进一步发现∠DOE+∠BAC=180°，所以，A、D、O、E四点共圆得证。最后，由“点到线的距离，垂线段最短”，即可求得CO的最小值。

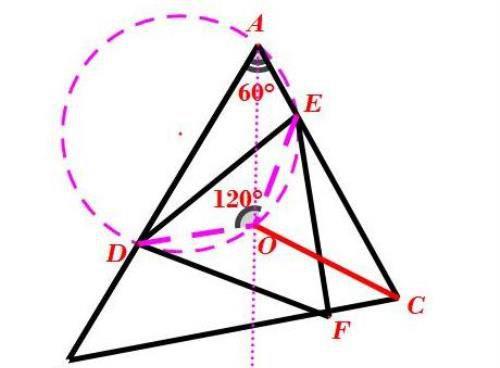
三、解答

感谢关注！欢迎留言！欢迎评论！

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请与我联系，一经查实立刻删除内容。本文内容由快快网络小故创作整理编辑！