边缘概率密度函数的简单理解是什么(边缘概率密度函数的简单理解方法)

导语：边缘概率密度函数的简单理解

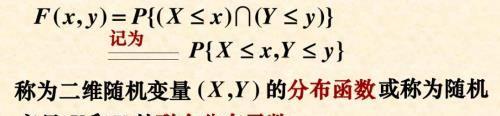
首先看边缘概率密度的定义：

图1

图2

图3

从定义可以看出，二维分布函数对于自变量来说，是一个范围。

图4

图5

图4图5的边缘分布函数定义表明，首先两个自变量也有一个变化范围，但对于x的边缘分布来说，y的取值则是它的全部定义域，反过来也一样。

图6

图7

图6图7给出了边缘分布函数和边缘密度函数的定义对比，可以清楚地看到，x的边缘分布函数x的取值是一个范围，但x的边缘密度函数中，x的取值则是一个固定的值，这一区别是和概率的分布函数与密度函数的定义完全相符的，因为概率密度函数f(x)指的就是在x固定的情况下，x的这个值的取值频度。

图8

图9

图8图9是由二维分布函数求边缘分布函数的例子。当然，边缘分布函数有了，边缘密度函数就得出来了。

图10

图10是由二维密度函数求边缘密度函数的例子。

注意两者的区别。图8图9中F(x,y)里面的x,y代表的是一个范围，图10中f(x,y)里面的x,y代表的则是一个固定的值。边缘密度fX则表示x固定，y变化。

图11

图12

图13

对于离散型变量来说，其边缘分布率指的是它的边缘密度函数。

下面是一个常用的正态分布的例子。

简单总结一下：

1：二维分布函数两个自变量都是范围。

2：边缘分布函数两个自变量也都是范围，但其中一个范围固定，另一个则是全定义域。

3：边缘密度函数两个自变量其中一个是固定的值，另一个则是全定义域。

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请反馈，一经查实立刻删除内容。本文内容由快快网络小熊创作整理编辑！